题目内容
13.若直角三角形的两边a、b是方程x2-7x+12=0的两个根,则该直角三角形的内切圆的半径r=1或$\frac{{\sqrt{7}-1}}{2}$.分析 先求出方程的解,分为两种情况:当4为直角边或4为斜边,求出第三边,代入公式内切圆半径r=$\frac{a+b-c}{2}$(a、b为直角边,c为斜边)求出即可.
解答 解:解方程x2-7x+12=0得:x1=3,x2=4,
设a=3,b=4,
当b=4是直角边时,斜边为$\sqrt{{3}^{2}+{4}^{2}}$=5,
该直角三角形的内切圆的半径r=$\frac{3+4-5}{2}$=1;
当b=4是斜边时,另一直角边为$\sqrt{{4}^{2}-{3}^{2}}$=$\sqrt{7}$,
该直角三角形的内切圆的半径r=$\frac{3+\sqrt{7}-4}{2}$=$\frac{\sqrt{7}-1}{2}$;
故答案为:1或$\frac{\sqrt{7}-1}{2}$.
点评 本题考查了勾股定理,解一元二次方程,三角形的内切圆与内心等知识点,能求出符合的所有情况是解此题的关键,注意:直角三角形内切圆半径r=$\frac{a+b-c}{2}$(a、b为直角边,c为斜边).

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
3.在-1,$\frac{1}{3}$,$\sqrt{2}$,0.7中,无理数是( )
| A. | -1 | B. | $\frac{1}{3}$ | C. | $\sqrt{2}$ | D. | 0.7 |
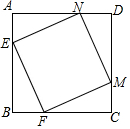 如图,E,F,M,N分别是边长为4的正方形ABCD四条边上的点,且AE=BF=CM=DN.那么四边形EFMN的面积的最小值是8.
如图,E,F,M,N分别是边长为4的正方形ABCD四条边上的点,且AE=BF=CM=DN.那么四边形EFMN的面积的最小值是8. 如图,在四边形ABCD中,AD∥BC,∠ABC的平分线交CD于点E.
如图,在四边形ABCD中,AD∥BC,∠ABC的平分线交CD于点E.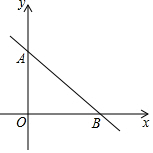 如图,直线y=-$\frac{3}{4}$x+3与x轴、y轴分别交于点B、A,在x轴上有点P,使得AB=BP,则点P的坐标为(9,0)或(-1,0).
如图,直线y=-$\frac{3}{4}$x+3与x轴、y轴分别交于点B、A,在x轴上有点P,使得AB=BP,则点P的坐标为(9,0)或(-1,0). 如图,在矩形ABCD中,点E,F分别是AB,CD的中点,连结DE,BF,分别取DE,BF的中点M,N,连结AM,CN,MN,若AB=2$\sqrt{3}$,BC=2$\sqrt{5}$,则图中阴影部分图形的面积和为2$\sqrt{15}$.
如图,在矩形ABCD中,点E,F分别是AB,CD的中点,连结DE,BF,分别取DE,BF的中点M,N,连结AM,CN,MN,若AB=2$\sqrt{3}$,BC=2$\sqrt{5}$,则图中阴影部分图形的面积和为2$\sqrt{15}$.