题目内容
1.已知:a=2+$\sqrt{5}$,b=2-$\sqrt{5}$,求a2-ab-b2的值.分析 直接利用平方差公式分解因式,进而将已知代入求出即可.
解答 解:a2-ab-b2=(a+b)(a-b)-ab
将a=2+$\sqrt{5}$,b=2-$\sqrt{5}$,代入上式得:
原式=(2+$\sqrt{5}$+2-$\sqrt{5}$)(2+$\sqrt{5}$-2+$\sqrt{5}$)-(2+$\sqrt{5}$)(2-$\sqrt{5}$)
=4×2$\sqrt{5}$-(4-5)
=8$\sqrt{5}$+1.
点评 此题主要考查了二次根式的化简求值,正确应用乘法公式是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.在△ABC中,AB=8,∠ABC=30°,AC=5,则BC的长为( )
| A. | 4$\sqrt{3}$ | B. | 4$\sqrt{3}$+3 | C. | 4$\sqrt{3}$-3 | D. | 4$\sqrt{3}$+3或4$\sqrt{3}$-3 |
11.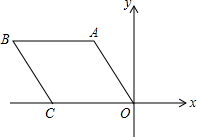 菱形AOCB在平面直角坐标系中的位置如图,若OA=2,∠AOC=45°,则B点的坐标是( )
菱形AOCB在平面直角坐标系中的位置如图,若OA=2,∠AOC=45°,则B点的坐标是( )
 菱形AOCB在平面直角坐标系中的位置如图,若OA=2,∠AOC=45°,则B点的坐标是( )
菱形AOCB在平面直角坐标系中的位置如图,若OA=2,∠AOC=45°,则B点的坐标是( )| A. | (-2-$\sqrt{2}$,$\sqrt{2}$) | B. | (-2+$\sqrt{2}$,$\sqrt{2}$) | C. | (2+$\sqrt{2}$,$\sqrt{2}$) | D. | (2-$\sqrt{2}$,$\sqrt{2}$) |
 如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.
如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.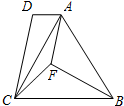 如图,在四边形ABCD中,AB=BC,BF是∠ABC的平分线,CA是∠DCF的平分线.求证:AF∥DC.
如图,在四边形ABCD中,AB=BC,BF是∠ABC的平分线,CA是∠DCF的平分线.求证:AF∥DC.