题目内容
20.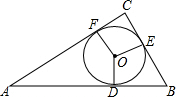 如图,在Rt△ABC中,∠C=90°,⊙O是△ABC的内切圆,切点D、E、F,
如图,在Rt△ABC中,∠C=90°,⊙O是△ABC的内切圆,切点D、E、F,(1)求证:四边形OECF是正方形;
(2)若AF=10,BE=3,求⊙O的面积.
分析 (1)连接OE、OF、OD,由切线的性质得到∠OGC=∠OEC=∠C=90°,从而可证四边形OECF是矩形,然后由OE=OF,可知:四边形OECF是正方形;
(2)由切线长定理可求得AB=AF+BE=13,设圆的半径为r,则AC=10+r,BC=3+r,最后由勾股定理求列方程求解即可.
解答 解:(1)∵点E、F是圆的切点,
∴OE⊥BC,OF⊥AC.
∴∠OFC=∠OEC=∠C=90°.
∴四边形OECF是矩形.
∵OE=OF,
∴四边形OECF是正方形.
(2)∵⊙O是△ABC的内切圆,
∴AF=AD,BE=DB.
∴AB=AD+BD=10+3=13.
设圆O的半径为r,则AC=10+r,BC=3+r.
在Rt△ABC中,由勾股定理得;AC2+BC2=AB2,即(10+r)2+(r+3)2=132.
解得:r=2或r=-15(舍去).
∴⊙O的面积=4π.
点评 本题主要考查的是切线的性质、切线长定理、正方形的判定、勾股定理的应用,根据切线长定理和勾股定理列出关于r的方程是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.如果关于x的方程(m-2)${x}^{{m}^{2}-2}$-2x-12=0是关于x的一元二次方程,那么m的值为( )
| A. | ±2 | B. | 2 | C. | -2 | D. | 都不对 |
5.一元二次方程x2+x-2=0的两根是( )
| A. | x1=1,x2=2 | B. | x1=-1,x2=-2 | C. | x1=1,x2=-2 | D. | x1=-1,x2=2 |
12.下列各式中是二元一次方程组的是( )
| A. | $\left\{\begin{array}{l}{x+y=3}\\{z+x=5}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=5}\\{{y}^{2}=4}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x+y=4}\\{\frac{1}{x}+\frac{1}{y}=9}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=y+11}\\{2x=y}\end{array}\right.$ |
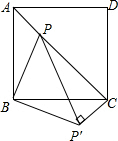 如图所示,点P是正方形ABCD内的一点,连接AP,BP,CP,将△PAB绕着点B顺时针旋转90°到△P′CB的位置.若AP=2,BP=4,∠APB=135°,求PP′及PC的长.
如图所示,点P是正方形ABCD内的一点,连接AP,BP,CP,将△PAB绕着点B顺时针旋转90°到△P′CB的位置.若AP=2,BP=4,∠APB=135°,求PP′及PC的长.