题目内容
根据下列情境编制一个实际问题,说出其中的常量与变量,并说明变量的取值范围:
小王春节骑车去看望爷爷,小王家与爷爷家相距10千米,小王骑车的速度为每小时12千米.
小王春节骑车去看望爷爷,小王家与爷爷家相距10千米,小王骑车的速度为每小时12千米.
考点:常量与变量
专题:
分析:根据函数的定义,需要有两个变量,可以从小王与爷爷家的距离和时间考虑求解.
解答:解:设小王与爷爷家的距离为s,出发时间为t,
则s=-12t+10,
-12与10是常量,s与t是变量,
∵s≥0,即-12t+10≥0,
∴t≤
,
t的取值范围是0≤t≤
,
s的取值范围是0≤s≤10.
则s=-12t+10,
-12与10是常量,s与t是变量,
∵s≥0,即-12t+10≥0,
∴t≤
| 5 |
| 6 |
t的取值范围是0≤t≤
| 5 |
| 6 |
s的取值范围是0≤s≤10.
点评:本题考查了常量与变量,难点在于理解函数的定义:设x和y是两个变量,D是实数集的某个子集,若对于D中的每个值x,变量y按照一定的法则有一个确定的值y与之对应,称变量y为变量x的函数,记作y=f(x);变量是指在程序的运行过程中随时可以发生变化的量.

练习册系列答案
相关题目
用公式法解方程x2-2=-3x时,a,b,c的值依次是( )
| A、0,-2,-3 |
| B、1,3,-2 |
| C、1,-3,-2 |
| D、1,-2,-3 |
下列语句中不正确的是( )
| A、斜边和一锐角对应相等的两个直角三角形全等 |
| B、有两边对应相等的两个直角三角形全等 |
| C、有两个锐角相等的两个直角三角形全等 |
| D、有一直角边和一锐角对应相等的两个直角三角形全等 |
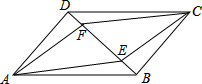 如图,已知在?ABCD中,E,F是对角线BD上的两点,则以下条件不能判断四边形AECF为平行四边形的是( )
如图,已知在?ABCD中,E,F是对角线BD上的两点,则以下条件不能判断四边形AECF为平行四边形的是( )| A、BE=DF |
| B、AF⊥BD,CE⊥BD |
| C、∠BAE=∠DCF |
| D、AF=CE |
有下列方程:
①x2-2x=0;②9x2-25=0;③(2x-1)2=1;④
(x+3)2=27.
其中能用直接开平方法做的是( )
①x2-2x=0;②9x2-25=0;③(2x-1)2=1;④
| 1 |
| 3 |
其中能用直接开平方法做的是( )
| A、①②③ | B、②③ |
| C、②③④ | D、①②③④ |
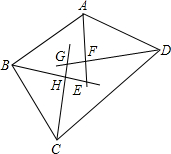 四边形ABCD的四个内角的平分线两两相交叉形成一个四边形EFGH,求证:
四边形ABCD的四个内角的平分线两两相交叉形成一个四边形EFGH,求证: