题目内容
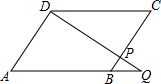如图，已知点P是?ABCD的边BC上的一点，连接OP并延长交AB的延长线于点Q，（1）若
| BP |
| PC |
| 1 |
| 4 |
| AB |
| AQ |
（2）若点P为BC边上的任意一点，设
| BC |
| BP |
| AB |
| BQ |
考点：相似三角形的判定与性质,平行四边形的性质
专题：
分析：（1）利用平行四边形的性质得平行，可得到△QPB∽△DPC，可得到CD和BQ的关系，从而可求得AB和AQ的比值；
（2）由相似可得
=
，结合平行四边形的性质，可找到
和
的关系，从而找到m和n之间的关系．
（2）由相似可得
| DC |
| BQ |
| PC |
| PB |
| BC |
| BP |
| AB |
| BQ |
解答：解：（1）∵四边形ABCD为平行四边形，
∴AB=CD，AB∥CD，
∴△QPB∽△DPC，
∴
=
=
，
∴DC=4BQ，即AB=4BQ，
∴
=
=
；
（2）猜想：m-n=1，
理由：由△DPC∽△QPB，得
=
，
∴
=
，
∴
=
=1+
=1+
，
即m=n=1．
∴AB=CD，AB∥CD，
∴△QPB∽△DPC，
∴
| BQ |
| CD |
| BP |
| CP |
| 1 |
| 4 |
∴DC=4BQ，即AB=4BQ，
∴
| AB |
| AQ |
| 4BQ |
| 4BQ+BQ |
| 4 |
| 5 |
（2）猜想：m-n=1，
理由：由△DPC∽△QPB，得
| DC |
| BQ |
| PC |
| PB |
∴
| AB |
| BQ |
| PC |
| BP |
∴
| BC |
| BP |
| BP+PC |
| BP |
| PC |
| BP |
| AB |
| BQ |
即m=n=1．
点评：本题主要考查相似三角形的判定和性质及平行四边形的性质，掌握相似三角形的对应边成比例是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
如图，△ABC中，∠C=45°，若MP和NQ分别垂直平分AB和AC，CQ=4，PQ=3，求BC的长．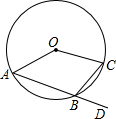
如图，A、B、C是⊙O上三点，D是AB延长线上一点，∠CBD=65°，则∠AOC=若|a|=1，b2=4，且ab＜0，则a-b的值是（ ）
| A、-3或3 | B、-1或3 |
| C、3 | D、-3 |