题目内容
5.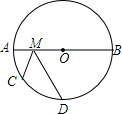 如图,AB是⊙O的直径,AB=8,$\widehat{AB}=2\widehat{AD}$=6$\widehat{AC}$,M是AB上一动点,则CM+DM的最小值( )
如图,AB是⊙O的直径,AB=8,$\widehat{AB}=2\widehat{AD}$=6$\widehat{AC}$,M是AB上一动点,则CM+DM的最小值( )| A. | 8 | B. | 6 | C. | 2+2$\sqrt{7}$ | D. | 4$\sqrt{3}$ |
分析 作点C关于AB的对称点C′,连接C′D与AB相交于点M,根据轴对称确定最短路线问题,点M为CM+DM的最小值时的位置,由AB是⊙O的直径,$\widehat{AB}=2\widehat{AD}$=6$\widehat{AC}$,求得$\widehat{AC}=\frac{1}{2}\widehat{CD}$,根据轴对称的性质得到$\widehat{AC}=\widehat{AC′}$,于是得到$\widehat{C′C}=\widehat{CD}$,根据垂径定理得到OC⊥C′D,C′D=2DN,解直角三角形即可得到结论.
解答  解:如图,作点C关于AB的对称点C′,连接C′D与AB相交于点M,
解:如图,作点C关于AB的对称点C′,连接C′D与AB相交于点M,
此时,点M为CM+DM的最小值时的位置,连接OC交C′D于N,连接OD,
∵AB是⊙O的直径,$\widehat{AB}=2\widehat{AD}$=6$\widehat{AC}$,
∴$\widehat{AC}=\frac{1}{2}\widehat{CD}$,
∵$\widehat{AC}=\widehat{AC′}$,
∴$\widehat{C′C}=\widehat{CD}$,
∴OC⊥C′D,C′D=2DN,
∴∠COD=60°,∴∠D=30°,
∵AB=8,
∴OD=4,∴DN=OD•sin60°=2$\sqrt{3}$,
∴C′D=4$\sqrt{3}$.
∴CM+DM的最小值=4$\sqrt{3}$.
故选D.
点评 本题考查了轴对称确定最短路线问题,垂径定理,熟记定理并作出图形,判断出CM+DM的最小值等于C′D是解题的关键.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
17.下列说法正确的是( )
| A. | 过A、B两点的直线的长度是A、B两点之间的距离 | |
| B. | 线段AB就是A、B两点之间的距离 | |
| C. | 在A、B两点之间的所有连线中,其中最短线的长度是A、B两点的距离 | |
| D. | 乘火车从石家庄到北京要走283千米,是说石家庄与北京的距离是283千米 |
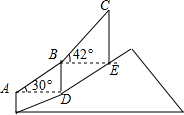 如图,登山缆车从点A出发,途径点B后到达终点C,其中AB段与BC段的运行路程均为200m,且AB段的运行路线与水平面的夹角为30°,BC段的运行路线与水平面的夹角为42°,求缆车从点A运行到点C垂直上升的距离.(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90).
如图,登山缆车从点A出发,途径点B后到达终点C,其中AB段与BC段的运行路程均为200m,且AB段的运行路线与水平面的夹角为30°,BC段的运行路线与水平面的夹角为42°,求缆车从点A运行到点C垂直上升的距离.(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90). 2015年4月1日起西安市市区出租车执行新运价标准,新运价标准如公示牌所示:
2015年4月1日起西安市市区出租车执行新运价标准,新运价标准如公示牌所示: 如图,点F、C在BE上,AB∥DE,∠A=∠D,BF=CE,求证:AB=DE.
如图,点F、C在BE上,AB∥DE,∠A=∠D,BF=CE,求证:AB=DE.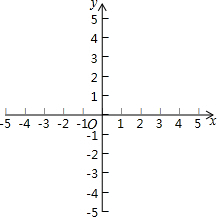 我们已经知道y=ax2+c的图象可以由函数y=ax2通过上、下平侈所得,例如,函数y=$\frac{1}{2}$x2-2的图象可以由函数y=$\frac{1}{2}$x2-2的图象可以由函数y=$\frac{1}{2}$x2的图象通过向下平移2个单位长度而得到,那么函数y=$\frac{1}{2}$(x-2)2的图象是否可由函数y=$\frac{1}{2}$x2的图象平移而得到呢?请在图中试一试,你能从中发现什么规律吗?
我们已经知道y=ax2+c的图象可以由函数y=ax2通过上、下平侈所得,例如,函数y=$\frac{1}{2}$x2-2的图象可以由函数y=$\frac{1}{2}$x2-2的图象可以由函数y=$\frac{1}{2}$x2的图象通过向下平移2个单位长度而得到,那么函数y=$\frac{1}{2}$(x-2)2的图象是否可由函数y=$\frac{1}{2}$x2的图象平移而得到呢?请在图中试一试,你能从中发现什么规律吗?