题目内容
在Rt△ABC中,∠C=90°,根据下列条件解直角三角形.(角度精确到1′,边长精确到0.1)
(1)a=20,∠B=60°;
(2)a=15,b=20.
(1)a=20,∠B=60°;
(2)a=15,b=20.
考点:解直角三角形
专题:
分析:(1)根据a和cosB即可求得c的值,即可求得b的值,即可解题;
(2)根据a、b的值可求得c的值,即可求得∠A,∠B的值,即可解题.
(2)根据a、b的值可求得c的值,即可求得∠A,∠B的值,即可解题.
解答:解:(1)∵∠B=60°,
∴∠A=30°,
∴cosB=
,
∴
=
,
∴c=40,b=
=20
;
(2)a=15,b=20,
∴c=
=25,
∴sinA=
,
∴∠A=36.9°,
∠B=53.1°.
∴∠A=30°,
∴cosB=
| 1 |
| 2 |
∴
| a |
| c |
| 1 |
| 2 |
∴c=40,b=
| c2-a2 |
| 3 |
(2)a=15,b=20,
∴c=
| b2+a2 |
∴sinA=
| 3 |
| 5 |
∴∠A=36.9°,
∠B=53.1°.
点评:本题考查了勾股定理的运用,考查了直角三角形中三角函数值的求解和运用,本题中每一问求c的值都是解题的关键.

练习册系列答案
相关题目
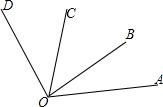 如图所示,∠AOB=35°,∠AOD=105°,∠COA=70°,试问在图中,哪条射线是哪个角的角平分线?
如图所示,∠AOB=35°,∠AOD=105°,∠COA=70°,试问在图中,哪条射线是哪个角的角平分线?