题目内容
15.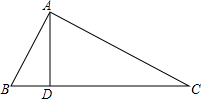 如图所示,在△ABC中,∠BAC=90°,AD⊥BC于点D,已知AB=6,BC=10,则tan∠BAD的值为$\frac{3}{4}$.
如图所示,在△ABC中,∠BAC=90°,AD⊥BC于点D,已知AB=6,BC=10,则tan∠BAD的值为$\frac{3}{4}$.
分析 由AD⊥BC得到∠ADB=90°,根据等角的余角相等得到∠C=∠BAD,在△ABC中,利用勾股定理可计算出AC,然后根据正切的定义得到tanC,即可得到tan∠BAD.
解答 解:∵AD⊥BC,
∴∠ADB=90°,
∴∠C=∠BAD,
在△ABC中,∠BAC=90°,AB=6,BC=10,
∴AC=$\sqrt{C{B}^{2}-A{B}^{2}}$=$\sqrt{1{0}^{2}-{6}^{2}}$=8,
∴tanC=$\frac{AB}{AC}$=$\frac{3}{4}$,
∴tan∠BAD=tanC=$\frac{AB}{AC}$=$\frac{3}{4}$.
故答案为$\frac{3}{4}$.
点评 本题考查了正切的定义:在直角三角形中,一锐角的正切等于它的对边与邻边的比值.也考查了勾股定理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.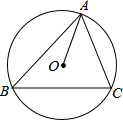 如图,△ABC内接于⊙O,∠B=∠OAC,OA=8cm,则AC=( )cm.
如图,△ABC内接于⊙O,∠B=∠OAC,OA=8cm,则AC=( )cm.
 如图,△ABC内接于⊙O,∠B=∠OAC,OA=8cm,则AC=( )cm.
如图,△ABC内接于⊙O,∠B=∠OAC,OA=8cm,则AC=( )cm.| A. | 16 | B. | 8$\sqrt{3}$ | C. | 8$\sqrt{2}$ | D. | 4$\sqrt{2}$ |
10.在Rt△ABC中,∠C=90°,tanB=$\frac{5}{3}$,则cosA=( )
| A. | $\frac{4}{5}$ | B. | $\frac{3}{4}$ | C. | $\frac{3\sqrt{34}}{34}$ | D. | $\frac{5\sqrt{34}}{34}$ |
20.某日嵊州的气温是7℃,长春的气温是-8℃,则嵊州的气温比长春的气温高( )
| A. | 15℃ | B. | -15℃ | C. | 1℃ | D. | -1℃ |
5. 如图,⊙O是△ABC的外接圆,∠BOC=80°,则∠A的度数等于( )
如图,⊙O是△ABC的外接圆,∠BOC=80°,则∠A的度数等于( )
 如图,⊙O是△ABC的外接圆,∠BOC=80°,则∠A的度数等于( )
如图,⊙O是△ABC的外接圆,∠BOC=80°,则∠A的度数等于( )| A. | 60° | B. | 50° | C. | 40° | D. | 30° |
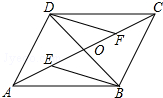 如图,四边形ABCD的对角线AC、BD交于点O,已知O是AC的中点,AE=CF,DF∥BE.
如图,四边形ABCD的对角线AC、BD交于点O,已知O是AC的中点,AE=CF,DF∥BE.