题目内容
8.在Rt△ABC中,∠C=90°,c=10,b=5,解这个三角形.分析 由sinB=$\frac{b}{c}$可得∠B,根据直角三角形两锐角互余得∠A,再根据勾股定理可得a.
解答 解:∵sinB=$\frac{b}{c}$=$\frac{5}{10}$=$\frac{1}{2}$,
∴∠B=30°,
∴∠A=90°-∠B=90°-30°=60°,
a=$\sqrt{{c}^{2}-{b}^{2}}$=$\sqrt{1{0}^{2}-{5}^{2}}$=5$\sqrt{3}$.
点评 本题考查了解直角三角形,主要利用了锐角三角函数和勾股定理.

练习册系列答案
相关题目
18.已知$\frac{3}{{x}^{2}+x}$-x2=2+x,则代数式2x2+2x的值是( )
| A. | 2 | B. | -6 | C. | 2或-6 | D. | -2或6 |
13. 如图,A、B两点在数轴上表示的数分别为a、b,下列式子成立的是( )
如图,A、B两点在数轴上表示的数分别为a、b,下列式子成立的是( )
 如图,A、B两点在数轴上表示的数分别为a、b,下列式子成立的是( )
如图,A、B两点在数轴上表示的数分别为a、b,下列式子成立的是( )| A. | a-b>0 | B. | a+b<0 | C. | -a+b>0 | D. | -a-b>0 |

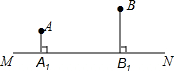 如图,直线MN表示一条铁路,A,B是两个城市,它们到铁路的垂直距离分别为AA1=20km,BB1=40km,已知A1B1=80km,现要在A1,B1之间设一个中转站P,使两个城市到中转站的距离之和最短,请你设计一种方案确定P点的位置,并求这个最短距离.
如图,直线MN表示一条铁路,A,B是两个城市,它们到铁路的垂直距离分别为AA1=20km,BB1=40km,已知A1B1=80km,现要在A1,B1之间设一个中转站P,使两个城市到中转站的距离之和最短,请你设计一种方案确定P点的位置,并求这个最短距离.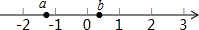 已知a、b在数轴上的位置如图,则a+b,a-b,b-a,-a-b中,最大的数是哪一个?
已知a、b在数轴上的位置如图,则a+b,a-b,b-a,-a-b中,最大的数是哪一个?