题目内容
如图,已知直线AB:y=kx+2k+4与抛物线y=
x2交于A,B两点.

(1)直线AB总经过一个定点C,请直接出点C坐标;
(2)当k=-
时,在直线AB下方的抛物线上求点P,使△ABP的面积等于5;
(3)若在抛物线上存在定点D使∠ADB=90°,求点D到直线AB的最大距离.
| 1 |
| 2 |

(1)直线AB总经过一个定点C,请直接出点C坐标;
(2)当k=-
| 1 |
| 2 |
(3)若在抛物线上存在定点D使∠ADB=90°,求点D到直线AB的最大距离.
考点:二次函数综合题,解一元二次方程-因式分解法,根与系数的关系,勾股定理,相似三角形的判定与性质
专题:压轴题
分析:(1)要求定点的坐标,只需寻找一个合适x,使得y的值与k无关即可.
(2)只需联立两函数的解析式,就可求出点A、B的坐标.设出点P的横坐标为a,运用割补法用a的代数式表示△APB的面积,然后根据条件建立关于a的方程,从而求出a的值,进而求出点P的坐标.
(3)设点A、B、D的横坐标分别为m、n、t,从条件∠ADB=90°出发,可构造k型相似,从而得到m、n、t的等量关系,然后利用根与系数的关系就可以求出t,从而求出点D的坐标.由于直线AB上有一个定点C,容易得到DC长就是点D到AB的最大距离,只需构建直角三角形,利用勾股定理即可解决问题.
(2)只需联立两函数的解析式,就可求出点A、B的坐标.设出点P的横坐标为a,运用割补法用a的代数式表示△APB的面积,然后根据条件建立关于a的方程,从而求出a的值,进而求出点P的坐标.
(3)设点A、B、D的横坐标分别为m、n、t,从条件∠ADB=90°出发,可构造k型相似,从而得到m、n、t的等量关系,然后利用根与系数的关系就可以求出t,从而求出点D的坐标.由于直线AB上有一个定点C,容易得到DC长就是点D到AB的最大距离,只需构建直角三角形,利用勾股定理即可解决问题.
解答:解:(1)∵当x=-2时,y=(-2)k+2k+4=4.
∴直线AB:y=kx+2k+4必经过定点(-2,4).
∴点C的坐标为(-2,4).
(2)∵k=-
,
∴直线的解析式为y=-
x+3.
联立
,
解得:
或
.
∴点A的坐标为(-3,
),点B的坐标为(2,2).
过点P作PQ∥y轴,交AB于点Q,
过点A作AM⊥PQ,垂足为M,
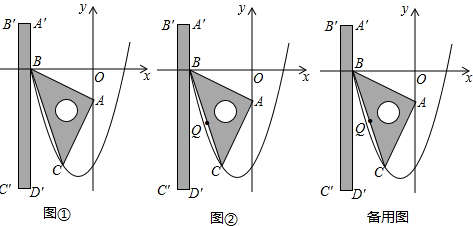
过点B作BN⊥PQ,垂足为N,如图1所示.

设点P的横坐标为a,则点Q的横坐标为a.
∴yP=
a2,yQ=-
a+3.
∵点P在直线AB下方,
∴PQ=yQ-yP
=-
a+3-
a2
∵AM+NB=a-(-3)+2-a=5.
∴S△APB=S△APQ+S△BPQ
=
PQ•AM+
PQ•BN
=
PQ•(AM+BN)
=
(-
a+3-
a2)•5
=5.
整理得:a2+a-2=0.
解得:a1=-2,a2=1.
当a=-2时,yP=
×(-2)2=2.
此时点P的坐标为(-2,2).
当a=1时,yP=
×12=
.
此时点P的坐标为(1,
).
∴符合要求的点P的坐标为(-2,2)或(1,
).
(3)过点D作x轴的平行线EF,
作AE⊥EF,垂足为E,
作BF⊥EF,垂足为F,如图2.

∵AE⊥EF,BF⊥EF,
∴∠AED=∠BFD=90°.
∵∠ADB=90°,
∴∠ADE=90°-∠BDF=∠DBF.
∵∠AED=∠BFD,∠ADE=∠DBF,
∴△AED∽△DFB.
∴
=
.
设点A、B、D的横坐标分别为m、n、t,
则点A、B、D的纵坐标分别为
m2、
n2、
t2.
AE=yA-yE=
m2-
t2.
BF=yB-yF=
n2-
t2.
ED=xD-xE=t-m,
DF=xF-xD=n-t.
∵
=
,
∴
=
.
∴
=
.
∵t≠m,t≠n,
∴
=
去分母并整理得:mn+(m+n)t+t2+4=0.
∵点A、B是直线AB:y=kx+2k+4与抛物线y=
x2交点,
∴m、n是方程kx+2k+4=
x2即x2-2kx-4k-8=0两根.
∴m+n=2k,mn=-4k-8.
∴-4k-8+2kt+t2+4=0,
即t2+2kt-4k-4=0.
即(t-2)(t+2k+2)=0.
∴t1=2,t2=-2k-2(舍).
∴定点D的坐标为(2,2).
过点D作x轴的平行线DG,
过点C作CG⊥DG,垂足为G,如图3所示.

∵点C(-2,4),点D(2,2),
∴CG=4-2=2,DG=2-(-2)=4.
∵CG⊥DG,
∴DC=
=
=
=2
.
过点D作DH⊥AB,垂足为H,如图3所示,
∴DH≤DC.
∴DH≤2
.
∴当DH与DC重合即DC⊥AB时,
点D到直线AB的距离最大,最大值为2
.
∴点D到直线AB的最大距离为2
.
∴直线AB:y=kx+2k+4必经过定点(-2,4).
∴点C的坐标为(-2,4).
(2)∵k=-
| 1 |
| 2 |
∴直线的解析式为y=-
| 1 |
| 2 |
联立
|
解得:
|
|
∴点A的坐标为(-3,
| 9 |
| 2 |
过点P作PQ∥y轴,交AB于点Q,
过点A作AM⊥PQ,垂足为M,
过点B作BN⊥PQ,垂足为N,如图1所示.

设点P的横坐标为a,则点Q的横坐标为a.
∴yP=
| 1 |
| 2 |
| 1 |
| 2 |
∵点P在直线AB下方,
∴PQ=yQ-yP
=-
| 1 |
| 2 |
| 1 |
| 2 |
∵AM+NB=a-(-3)+2-a=5.
∴S△APB=S△APQ+S△BPQ
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=5.
整理得:a2+a-2=0.
解得:a1=-2,a2=1.
当a=-2时,yP=
| 1 |
| 2 |
此时点P的坐标为(-2,2).
当a=1时,yP=
| 1 |
| 2 |
| 1 |
| 2 |
此时点P的坐标为(1,
| 1 |
| 2 |
∴符合要求的点P的坐标为(-2,2)或(1,
| 1 |
| 2 |
(3)过点D作x轴的平行线EF,
作AE⊥EF,垂足为E,
作BF⊥EF,垂足为F,如图2.

∵AE⊥EF,BF⊥EF,
∴∠AED=∠BFD=90°.
∵∠ADB=90°,
∴∠ADE=90°-∠BDF=∠DBF.
∵∠AED=∠BFD,∠ADE=∠DBF,
∴△AED∽△DFB.
∴
| AE |
| DF |
| ED |
| FB |
设点A、B、D的横坐标分别为m、n、t,
则点A、B、D的纵坐标分别为
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
AE=yA-yE=
| 1 |
| 2 |
| 1 |
| 2 |
BF=yB-yF=
| 1 |
| 2 |
| 1 |
| 2 |
ED=xD-xE=t-m,
DF=xF-xD=n-t.
∵
| AE |
| DF |
| ED |
| FB |
∴
| ||||
| n-t |
| t-m | ||||
|
∴
| (m+t)(m-t) |
| 2(n-t) |
| 2(t-m) |
| (n+t)(n-t) |
∵t≠m,t≠n,
∴
| m+t |
| 2 |
| -2 |
| n+t |
去分母并整理得:mn+(m+n)t+t2+4=0.
∵点A、B是直线AB:y=kx+2k+4与抛物线y=
| 1 |
| 2 |
∴m、n是方程kx+2k+4=
| 1 |
| 2 |
∴m+n=2k,mn=-4k-8.
∴-4k-8+2kt+t2+4=0,
即t2+2kt-4k-4=0.
即(t-2)(t+2k+2)=0.
∴t1=2,t2=-2k-2(舍).
∴定点D的坐标为(2,2).
过点D作x轴的平行线DG,
过点C作CG⊥DG,垂足为G,如图3所示.

∵点C(-2,4),点D(2,2),
∴CG=4-2=2,DG=2-(-2)=4.
∵CG⊥DG,
∴DC=
| GC2+DG2 |
=
| 22+42 |
=
| 20 |
=2
| 5 |
过点D作DH⊥AB,垂足为H,如图3所示,
∴DH≤DC.
∴DH≤2
| 5 |
∴当DH与DC重合即DC⊥AB时,
点D到直线AB的距离最大,最大值为2
| 5 |
∴点D到直线AB的最大距离为2
| 5 |
点评:本题考查了解方程组、解一元二次方程、一元二次方程根与系数的关系、勾股定理、相似三角形的性质与判定等知识,考查了通过解方程组求两函数交点坐标、用割补法表示三角形的面积等方法,综合性比较强.构造K型相似以及运用根与系数的关系是求出点D的坐标的关键,点C是定点又是求点D到直线AB的最大距离的突破口.

练习册系列答案
相关题目
已知:a2-3a+1=0,则a+
-2的值为( )
| 1 |
| a |
A、
| ||
| B、1 | ||
| C、-1 | ||
| D、-5 |

 某公司招聘人才,对应聘者分别进行阅读能力、思维能力和表达能力三项测试,其中甲、乙两人的成绩如下表(单位:分):
某公司招聘人才,对应聘者分别进行阅读能力、思维能力和表达能力三项测试,其中甲、乙两人的成绩如下表(单位:分): 如图,把抛物线y=
如图,把抛物线y=