题目内容
5.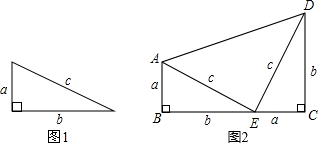 【定理表述】
【定理表述】请你根据图1中的直角三角形叙述勾股定理(用文字及符号语言叙述);
【尝试证明】
以图1中的直角三角形为基础,可以构造出以a、b为底,以a+b为高的直角梯形(如图2),请你利用图2,验证勾股定理;
【知识拓展】
利用图2中的直角梯形,我们可以证明$\frac{a+b}{c}$<$\sqrt{2}$.其证明步骤如下:
∵BC=a+b,AD=$\sqrt{2}$c.
又∵在直角梯形ABCD中有BC<AD(填大小关系),即a+b<$\sqrt{2}$c,
∴$\frac{a+b}{c}$<$\sqrt{2}$.
分析 【尝试证明】利用S梯形ABCD=SRt△ABE+SRt△DEC+SRt△AED进行证明即可;
【知识拓展】在直角梯形ABCD中,BC<AD,由于已证△AED是直角三角形,那么利用勾股定理有AD=$\sqrt{2}$c,从而可证$\frac{a+b}{c}$<$\sqrt{2}$.
解答 解:【定理表述】如果直角三角形的两直角边长分别为a、b,斜边长为c,那么a2+b2=c2.
【尝试证明】
∵Rt△ABE≌Rt△ECD,
∴∠AEB=∠EDC,
又∵∠EDC+∠DEC=90°,
∴∠AEB+∠DEC=90°,
∴∠AED=90°.
∵S梯形ABCD=SRt△ABE+SRt△DEC+SRt△AED,
∴$\frac{1}{2}$(a+b)(a+b)=$\frac{1}{2}$ab+$\frac{1}{2}$ab+$\frac{1}{2}$c2,
整理,得a2+b2=c2.
【知识拓展】
∵AD=$\sqrt{2}$c,BC<AD,
∴a+b<$\sqrt{2}$c,即$\frac{a+b}{c}$<$\sqrt{2}$,
故答案为:$\sqrt{2}$c,<,a+b<$\sqrt{2}$c
点评 本题考查了勾股定理的证明,本题利用了全等三角形的判定和性质、面积分割法、勾股定理等知识.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
15.某鞋店一天中卖出运动鞋11双,其中各种尺码的鞋的销售量如下表:
则这11双鞋的尺码组成的一组数据中,众数和中位数分别是25,25.
| 尺码(cm) | 23.5 | 24 | 24.5 | 25 | 25.5 |
| 销售量(双) | 1 | 2 | 2 | 5 | 1 |
16.下列条件中,不能判断四边形ABCD是平行四边形的是( )
| A. | AB=CD,AD∥BC | B. | AB∥CD,AB=CD | C. | AB=CD,AD=BC | D. | AB∥CD,AD∥BC |
13.要调查我校初中7000多名学生的视力情况,下列调查方式最合适的是( )
| A. | 在我校初一年级学生中随机选取100名女生 | |
| B. | 在我校初二年级学生中随机选取100名男生 | |
| C. | 在我校初三年级学生中随机选取100名学生 | |
| D. | 在我校7000多名初中学生中随机选取100名学生 |
14.如图,△ABC与△A′B′C′关于直线MN对称,P为MN上任意一点,下列说法不正确的是( )
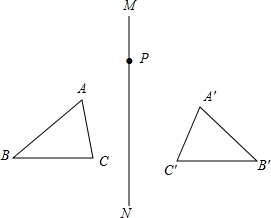

| A. | AP=A′P | B. | MN垂直平分AA′,CC′ | ||
| C. | 这两个三角形的面积相等 | D. | 直线AB、A′B的交点不一定在MN上 |
15.聪明好学的王明用计算机自己设计了一个计算程序,输入和输出的数据如下表:
那么,
(1)当输入数据10时,输出的数据是$\frac{10}{101}$.
(2)当输入数据n时,输出的数据是$\frac{n}{{n}^{2}+1}$(用n的代数式表示).
| 输入 | … | 1 | 2 | 3 | 4 | 5 | 6 | … |
| 输出 | … | $\frac{1}{2}$ | $\frac{2}{5}$ | $\frac{3}{10}$ | $\frac{4}{17}$ | $\frac{5}{26}$ | $\frac{6}{37}$ | … |
(1)当输入数据10时,输出的数据是$\frac{10}{101}$.
(2)当输入数据n时,输出的数据是$\frac{n}{{n}^{2}+1}$(用n的代数式表示).
 如图,点E为正方形ABCD的边BC延长线上一点,BF⊥DE于点F,交CD边于点G.
如图,点E为正方形ABCD的边BC延长线上一点,BF⊥DE于点F,交CD边于点G.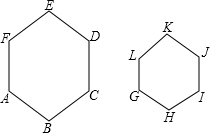 如图,六边形ABCDEF∽六边形GHIJKL,相似比为2:1,则下列结论中:
如图,六边形ABCDEF∽六边形GHIJKL,相似比为2:1,则下列结论中: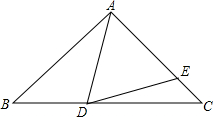 如图,△ABC是等腰三角形,AB=AC,D、E分别是△ABC的边BC、AC上的点,且AD=AE,若∠BAD=46°,则∠EDC=23°.
如图,△ABC是等腰三角形,AB=AC,D、E分别是△ABC的边BC、AC上的点,且AD=AE,若∠BAD=46°,则∠EDC=23°.