题目内容
6.对于实数a、b,定义一种新运算“?”为:a?b=$\frac{2}{{a}^{2}+ab}$,这里等式右边是通常的四则运算.例如:1?3=$\frac{2}{{1}^{2}+1×3}$=$\frac{1}{2}$.(1)解方程(-2)?x=1?x;
(2)若x,y均为自然数,且满足等式y-5=$\frac{1}{(-1)?x}$,求满足条件的所有数对(x,y).
分析 (1)所求方程利用题中的新定义化简,求出解即可;
(2)已知等式利用题中的新定义化简,整理得到x与y的方程,即可求出满足条件的所有数对(x,y).
解答 解:(1)根据题意,得$\frac{2}{4-2x}$=$\frac{2}{1+x}$,
去分母得:1+x=4-2x,
解得:x=1,
经检验x=1是分式方程的解;
(2)根据题意得:y-5=$\frac{1}{\frac{2}{1-x}}$,
整理得:x+2y=11,
∵x,y均为自然数,
∴$\left\{\begin{array}{l}{x=1}\\{y=5}\end{array}\right.$或$\left\{\begin{array}{l}{x=3}\\{y=4}\end{array}\right.$或$\left\{\begin{array}{l}{x=5}\\{y=3}\end{array}\right.$或$\left\{\begin{array}{l}{x=7}\\{y=2}\end{array}\right.$或$\left\{\begin{array}{l}{x=9}\\{y=1}\end{array}\right.$或$\left\{\begin{array}{l}{x=11}\\{y=0}\end{array}\right.$,
经检验,$\left\{\begin{array}{l}{x=1}\\{y=5}\end{array}\right.$不是原方程的解,
则满足条件的所有数对(x,y)为(3,4);(5,3);(7,2);(9,1);(11,0),共五对.
点评 此题考查了解分式方程,弄清题中的新定义是解本题的关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
16.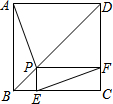 如图,P为正方形ABCD的对角线BD上任一点,过点P作PE⊥BC于点E,PF⊥CD于点F,连接EF.给出以下4个结论:①AP=EF;②AP⊥EF;③△APD一定是等腰三角形;④∠PFE=∠BAP.其中,所有正确的结论是( )
如图,P为正方形ABCD的对角线BD上任一点,过点P作PE⊥BC于点E,PF⊥CD于点F,连接EF.给出以下4个结论:①AP=EF;②AP⊥EF;③△APD一定是等腰三角形;④∠PFE=∠BAP.其中,所有正确的结论是( )
 如图,P为正方形ABCD的对角线BD上任一点,过点P作PE⊥BC于点E,PF⊥CD于点F,连接EF.给出以下4个结论:①AP=EF;②AP⊥EF;③△APD一定是等腰三角形;④∠PFE=∠BAP.其中,所有正确的结论是( )
如图,P为正方形ABCD的对角线BD上任一点,过点P作PE⊥BC于点E,PF⊥CD于点F,连接EF.给出以下4个结论:①AP=EF;②AP⊥EF;③△APD一定是等腰三角形;④∠PFE=∠BAP.其中,所有正确的结论是( )| A. | ①② | B. | ①③ | C. | ①②④ | D. | ①③④ |
17.若关于x的一元一次不等式组$\left\{\begin{array}{l}{x-a>0}\\{2x-2<1-x}\end{array}\right.$有解,则a的取值范围是( )
| A. | a>1 | B. | a≥1 | C. | a<1 | D. | a≤1 |
11.|-1|的结果为( )
| A. | 1 | B. | ±1 | C. | -1 | D. | 无法确定 |
 已知:如图,点C是AB的中点,AD=CE,CD=BE.求证:CD∥BE.
已知:如图,点C是AB的中点,AD=CE,CD=BE.求证:CD∥BE. 一天早上,马虎同学上学,到校后发现文具盒落在家里,此时离上课开始还有25分钟,于是立即步行回家取文具盒,同时,他爸爸从家里出发骑自行车以他3倍的速度给他送文具盒,两人在途中相遇,相遇后马虎立即坐父亲的自行车赶回学校.如图中线段AB、OB分别表示父子俩在送文具盒过程中,离学校的路程S(米)与所用时间t(分钟)之间的函数关系,结合图象解答下列问题(假设骑自行车和步行的速度始终保持不变);
一天早上,马虎同学上学,到校后发现文具盒落在家里,此时离上课开始还有25分钟,于是立即步行回家取文具盒,同时,他爸爸从家里出发骑自行车以他3倍的速度给他送文具盒,两人在途中相遇,相遇后马虎立即坐父亲的自行车赶回学校.如图中线段AB、OB分别表示父子俩在送文具盒过程中,离学校的路程S(米)与所用时间t(分钟)之间的函数关系,结合图象解答下列问题(假设骑自行车和步行的速度始终保持不变);