题目内容
1. 如图,在△ABC中,AB=AC,∠B=50°,P边AB上的一个动点(不与顶点A重合),则∠BPC的值可能是( )
如图,在△ABC中,AB=AC,∠B=50°,P边AB上的一个动点(不与顶点A重合),则∠BPC的值可能是( )| A. | 135° | B. | 85° | C. | 50° | D. | 40° |
分析 根据等边对等角可得∠B=∠ACB=50°,再根据三角形内角和计算出∠A的度数,然后根据三角形内角与外角的关系可得∠BPC>∠A,进而可得答案.
解答 解:∵AB=AC,
∴∠B=∠ACB=50°,
∴∠A=180°-50°×2=80°,
∵∠BPC=∠A+∠ACP,
∴∠BPC>∠A,
∴∠BPC>80°,
故选:B.
点评 此题主要考查了等腰三角形的性质,关键是掌握等腰三角形两底角相等.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
11. 如图,AB是⊙O的直径,BC是⊙O的弦,若∠AOC=80°,则∠B的度数为( )
如图,AB是⊙O的直径,BC是⊙O的弦,若∠AOC=80°,则∠B的度数为( )
 如图,AB是⊙O的直径,BC是⊙O的弦,若∠AOC=80°,则∠B的度数为( )
如图,AB是⊙O的直径,BC是⊙O的弦,若∠AOC=80°,则∠B的度数为( )| A. | 30° | B. | 35° | C. | 40° | D. | 45° |
16.已知一组数据:12,5,9,5,14,下列说法不正确的是( )
| A. | 平均数是9 | B. | 中位数是9 | C. | 方差是12 | D. | 众数是5 |
10.若3a7xby+7与2a14b2x是同类项,则yx的值是( )
| A. | -9 | B. | -6 | C. | 6 | D. | 9 |
11.如果m是任意实数,那么点M(m-5,m+2)一定不在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 ”表示数据输入、输出框;用“
”表示数据输入、输出框;用“ ”表示数据处理和运算框;用“
”表示数据处理和运算框;用“ ”表示数据判断框(根据条件决定执行两条路径中的某一条)
”表示数据判断框(根据条件决定执行两条路径中的某一条)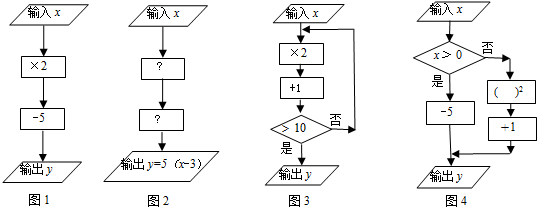
 ”内,应填-3;第二个运算框“
”内,应填-3;第二个运算框“ ”内,应填×5;
”内,应填×5;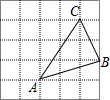 如图,每个小方格都是边长为1个单位的小正方形,A,B,C三点都是格点(每个小方格的顶点叫格点).
如图,每个小方格都是边长为1个单位的小正方形,A,B,C三点都是格点(每个小方格的顶点叫格点).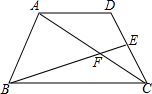 如图,梯形ABCD中,AD∥BC,BC=2AD,点E为边DC的中点,BE交AC于点F.求:
如图,梯形ABCD中,AD∥BC,BC=2AD,点E为边DC的中点,BE交AC于点F.求: