题目内容
在平面直角坐标系中,点P(2,-3),点M、N在反比例函数y=
的图象上,点N在点M的左侧,若以点O、P、M、N组成的四边形是平行四边形,求点N的坐标.
| 3 |
| x |
考点:反比例函数综合题
专题:
分析:分当OP∥MN和当MN与OP互相平分两种情况进行讨论,当OP∥MN时即可表示出M的坐标,即可列方程求得,利用方程即可求解,当当MN与OP互相平分时,OP的中点就是MN的中点,根据中点公式求解.
解答: 解:当OP∥MN,且OP=MN时如图(1),设N(x,
解:当OP∥MN,且OP=MN时如图(1),设N(x,
),
∵P(2,-3),O(0,0)则M(x+2,
-3).
∴
-3=
+2,
∴x2+2x-2=0,x=-1+
或x=-1-
.
∴N(-1+
,3
+
)或N(-1-
,
)
当MN与OP互相平分时,
如图(2)OP的中点(1,-
)也是MN的中点,
设N(x,
),由此得,M(2-x,-3-
),
∴-3-
=
-x,
∴x=1+
或x=1-
.
∴N(1+
,
)或N(1-
,-
)
∴点N的坐标是N1(-1+
,
),N2(-1-
,
),N3(1+
,
),N4(1-
,-
).
 解:当OP∥MN,且OP=MN时如图(1),设N(x,
解:当OP∥MN,且OP=MN时如图(1),设N(x,| 3 |
| x |
∵P(2,-3),O(0,0)则M(x+2,
| 3 |
| x |
∴
| 3 |
| x |
| 3 |
| x |
∴x2+2x-2=0,x=-1+
| 3 |
| 3 |
∴N(-1+
| 3 |
| 3 |
| 3 |
| 2 |
| 3 |
6-3
| ||
| 2 |
当MN与OP互相平分时,
如图(2)OP的中点(1,-
| 3 |
| 2 |
设N(x,
| 3 |
| x |
| 3 |
| x |
∴-3-
| 3 |
| x |
| 3 |
| 2 |

∴x=1+
| 3 |
| 3 |
∴N(1+
| 3 |
6
| ||
| 2 |
| 3 |
6+3
| ||
| 2 |
∴点N的坐标是N1(-1+
| 3 |
6
| ||
| 2 |
| 3 |
6-3
| ||
| 2 |
| 3 |
6
| ||
| 2 |
| 3 |
6+3
| ||
| 2 |
点评:本题是反比例函数与平行四边形的综合应用,利用了一边平行且相等的四边形是平行四边形,以及对角线互相平分的四边形是平行四边形,正确进行讨论是关键.

练习册系列答案
相关题目
 如图所示,已知点E在AC上,点D在AB上,△ADC≌△EDB,且∠DEA=∠A,若∠A:∠C=5:3,请你求出∠EDC的度数.
如图所示,已知点E在AC上,点D在AB上,△ADC≌△EDB,且∠DEA=∠A,若∠A:∠C=5:3,请你求出∠EDC的度数.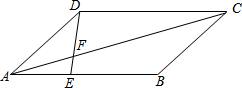 已知如图:?ABCD中,AE:EB=1:2,S△AEF=6cm2
已知如图:?ABCD中,AE:EB=1:2,S△AEF=6cm2