题目内容
9.在四边形ABCD中,AD=a,CD=b,点E在射线BA上,点F在射线BC上.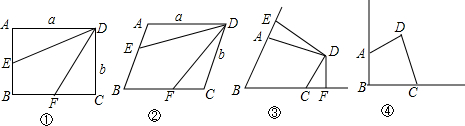
观察计算:
(1)如图①,若四边形ABCD是矩形,E是AB的中点.F是BC的中点,则四边形DEBF 的面积S四边形DEBF=$\frac{1}{2}$ab.
(2)若四边形ABCD是平行四边形,E是AB的中点,F是BC的中点,则S四边形DEBF:S四边形ABCD=1:2.
(3)如图②,若四边形ABCD是平行四边形,且BE:AB=2:3,BF:BC=2:3,则S四边形DEBF:S四边形ABCD=2:3.
探索规律:
如图③,在四边形ABCD中,若BE:AB=n:m,BF:BC=n:m,试猜想S四边形DEBF:S四边形ABCD=n:m,请说明理由.
解决问题:如图④,某小区角落有一四边形空地,为了充分利用空间,美化环境,想把它沿两侧墙壁改造为一块绿地,使绿地面积是原空地面积的3倍.请分别在两侧墙壁上确定点E、F,画出改造线DE、DF,并写出作法.
分析 (1)连接BD,根据三角形的中线把三角形分为面积相等的两部分和矩形的面积公式解答即可;
(2)由(1)的结论进行解答;
(3)根据高相等的两个三角形面积之比等于底的比进行解答即可,仿照观察计算的计算过程解答探索规律问题.
解答 
 解:(1)如图①,连接BD,
解:(1)如图①,连接BD,
∵E是AB的中点,∴S△DEB=$\frac{1}{2}$S△DAB,
∵F是BC的中点,∴S△FDB=$\frac{1}{2}$S△DCB,
∴S四边形DEBF=$\frac{1}{2}$S矩形ABCD=$\frac{1}{2}$ab,
故答案为:$\frac{1}{2}$ab;
(2)由(1)得,S四边形DEBF:S矩形ABCD=1:2,
故答案为:1:2;
(3)如图②,连接BD,
∵BE:AB=2:3,∴S△DEB=$\frac{2}{3}$S△DAB,
∵BF:BC=2:3,∴S△FDB=$\frac{2}{3}$S△DCB,
∴S四边形DEBF=$\frac{2}{3}$S矩形ABCD,
∴S四边形DEBF:S矩形ABCD=2:3,
故答案为:2:3;
探索规律:如图③,由(3)得,S四边形DEBF=$\frac{n}{m}$S矩形ABCD,
∴S四边形DEBF:S矩形ABCD=n:m,
故答案为:n:m;
解决问题:如图④,在BA的延长线上取一点E,使EA=2AB,在BC的延长线上取一点F,使FC=2BC,连接DE、DF,则DE和DF即为所求.
点评 本题考查的是矩形、平行四边形以及三角形的面积计算,掌握高相等的两个三角形面积之比等于底的比是解题的关键.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
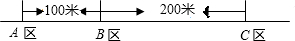 如图,某公司有三个住宅小区A,B,C,A,B,C各小区分别住有职工30人,15人,10人,且这三个小区在一条大道上(即A,B,C三点共线),已知AB=100米,BC=200米,为了方便职工上下班,该公司的接送车打算在某小区设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应该设在哪个小区?
如图,某公司有三个住宅小区A,B,C,A,B,C各小区分别住有职工30人,15人,10人,且这三个小区在一条大道上(即A,B,C三点共线),已知AB=100米,BC=200米,为了方便职工上下班,该公司的接送车打算在某小区设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应该设在哪个小区?
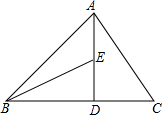 如图,在△ABC中,AD⊥BC于点D,AD=BD,DC=DE,∠C=60°,∠ABD=45°,求∠ABE的度数.
如图,在△ABC中,AD⊥BC于点D,AD=BD,DC=DE,∠C=60°,∠ABD=45°,求∠ABE的度数.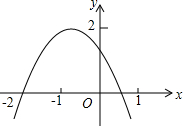 如图所示,二次函数y=ax2+bx+c(a≠0)的图象经过点(-1,2),且与x轴交点的横坐标分别为x1,x2,其中-2<x1<-1,0<x2<1,下列结论:①4a-2b+c<0;②2a-b<0;③c<2;④b2>4ac.其中正确的有( )
如图所示,二次函数y=ax2+bx+c(a≠0)的图象经过点(-1,2),且与x轴交点的横坐标分别为x1,x2,其中-2<x1<-1,0<x2<1,下列结论:①4a-2b+c<0;②2a-b<0;③c<2;④b2>4ac.其中正确的有( )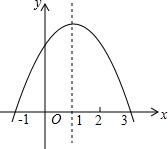 已知二次函数y=ax2+bx+c(a、b、c是常数),图象如图所示,则当x满足的条件是-1<x<3时,y>0.
已知二次函数y=ax2+bx+c(a、b、c是常数),图象如图所示,则当x满足的条件是-1<x<3时,y>0.