题目内容
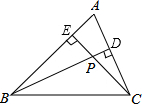 如图,在△ABC中,高BD和CE相交于点P.
如图,在△ABC中,高BD和CE相交于点P.(1)若∠A=60°,求∠DPE的度数;
(2)若∠A=α,∠DPE=β,试求α,β之间具有怎样的数量关系,并论证你的猜想.
考点:多边形内角与外角
专题:
分析:(1)根据高的定义,四边形内角和等于360°即可求解;
(2)根据高的定义,四边形内角和等于360°即可求解.
(2)根据高的定义,四边形内角和等于360°即可求解.
解答:解:∵高BD和CE相交于点P,
∴∠AEP=∠ADP=90°,
(1)∵∠A=60°,
∴∠DPE=360°-90°-90°-60°=120°;
(2)α+β=180°.
∵∠A=α,∠DPE=β,
∴α+β=360°-90°-90°=180°.
∴∠AEP=∠ADP=90°,
(1)∵∠A=60°,
∴∠DPE=360°-90°-90°-60°=120°;
(2)α+β=180°.
∵∠A=α,∠DPE=β,
∴α+β=360°-90°-90°=180°.
点评:考查了多边形内角与外角,关键是熟悉高的定义,四边形内角和等于360°的知识点.

练习册系列答案
相关题目
要组成一个三角形,三条线段长度可取( )
| A、3,4,8 |
| B、5,6,11 |
| C、2,2,3 |
| D、18,9,8 |
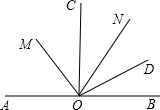 如图,∠AOC=90°,ON是锐角∠COD的平分线,OM是∠AOD的平分线,求∠MON的度数.
如图,∠AOC=90°,ON是锐角∠COD的平分线,OM是∠AOD的平分线,求∠MON的度数. 相框边的宽窄影响可放入相片的大小.如图,相框长26cm,宽22cm,相框边的宽xcm,相框内的面积为ycm2.
相框边的宽窄影响可放入相片的大小.如图,相框长26cm,宽22cm,相框边的宽xcm,相框内的面积为ycm2.