题目内容
10.菱形ABCD中,点P为CD上一点,连接BP.(1)如图1,若BP⊥CD,菱形ABCD边长为10,PD=4,连接AP,求AP的长.
(2)如图2,连接对角线AC、BD相交于点O,点N为BP的中点,过P作PM⊥AC于M,连接ON、MN.试判断△MON的形状,并说明理由.

分析 (1)在RT△BCP中利用勾股定理求出PB,在RT△ABP中利用勾股定理求出PA即可.
(2)如图2中,延长PM交BC于E.先证明PD=BE,再利用三角形中位线定理证明MN=$\frac{1}{2}$BE,ON=$\frac{1}{2}$PD即可.
解答 解: (1)如图1中,∵四边形ABCD是菱形,
(1)如图1中,∵四边形ABCD是菱形,
∴AB=BC=CD=AD=10,AB∥CD
∵PD=4,
∴PC=6,
∵PB⊥CD,
∴PB⊥AB,
∴∠CPB=∠ABP=90°,
在RT△PCB中,∵∠CPB=90°PC=6,BC=10,
∴PB=$\sqrt{B{C}^{2}-P{C}^{2}}$=$\sqrt{1{0}^{2}-{6}^{2}}$=8,
在RT△ABP中,∵∠ABP=90°,AB=10,PB=8,
∴PA=$\sqrt{A{B}^{2}+P{B}^{2}}$=$\sqrt{1{0}^{2}+{8}^{2}}$=2$\sqrt{41}$.
(2)△OMN是等腰三角形.
理由:如图2中,延长PM交BC于E.
∵四边形ABCD是菱形,
∴AC⊥BD,CB=CD,
∵PE⊥AC,
∴PE∥BD,
∴$\frac{PC}{CD}$=$\frac{CE}{CB}$,
∴CP=CE,
∴PD=BE,
∵CP=CE,CM⊥PE,
∴PM=ME,
∵PN=NB,
∴MN=$\frac{1}{2}$BE,
∵BO=OD,BN=NP,
∴ON=$\frac{1}{2}$PD,
∴ON=MN,
∴△OMN是等腰三角形.
点评 本题考查菱形的性质、平行线分线段成比例定理、三角形中位线定理等知识,解题的关键是添加辅助线构造,利用三角形中位线定理解决问题,属于中考常考题型.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
1.如图图形经过折叠,能围成正方体的是( )
| A. |  | B. |  | C. |  | D. |  |
18. 如图,AB是⊙O的切线,B为切点,AO与⊙O交于点C,若∠BAO=30°,则∠OCB的度数为( )
如图,AB是⊙O的切线,B为切点,AO与⊙O交于点C,若∠BAO=30°,则∠OCB的度数为( )
 如图,AB是⊙O的切线,B为切点,AO与⊙O交于点C,若∠BAO=30°,则∠OCB的度数为( )
如图,AB是⊙O的切线,B为切点,AO与⊙O交于点C,若∠BAO=30°,则∠OCB的度数为( )| A. | 30° | B. | 60° | C. | 50° | D. | 40° |
15. 如图,?ABCD的对角线交于点O,且AB=5,△OCD的周长为23,则?ABCD的两条对角线之和是( )
如图,?ABCD的对角线交于点O,且AB=5,△OCD的周长为23,则?ABCD的两条对角线之和是( )
 如图,?ABCD的对角线交于点O,且AB=5,△OCD的周长为23,则?ABCD的两条对角线之和是( )
如图,?ABCD的对角线交于点O,且AB=5,△OCD的周长为23,则?ABCD的两条对角线之和是( )| A. | 18 | B. | 28 | C. | 36 | D. | 46 |
2.下列各式从左到右,是因式分解的是( )
| A. | (x-2)(x-3)=(3-x)(2-x) | B. | x2y+xy2-1=xy(x+y)-1 | ||
| C. | a(x-3)+b(x-3)=(x-3)(a+b) | D. | (y-1)(y+1)=y2-1 |
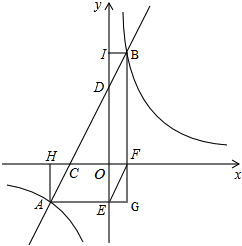 如图,一直线与反比例函数y=$\frac{k}{x}$(k>0)交于A、B两点,直线与x轴、y轴分别交于C、D两点,过A、B两点分别向x轴、y轴作垂线,H、E、F、I为垂足,连接EF,延长AE、BF相交于点G.
如图,一直线与反比例函数y=$\frac{k}{x}$(k>0)交于A、B两点,直线与x轴、y轴分别交于C、D两点,过A、B两点分别向x轴、y轴作垂线,H、E、F、I为垂足,连接EF,延长AE、BF相交于点G. 如图,在△ABC中,AB=AC,作AD⊥AB交BC的延长线于点D,作AE∥BD,CE⊥AC,且AE,CE相交于点E,求证:AD=CE.
如图,在△ABC中,AB=AC,作AD⊥AB交BC的延长线于点D,作AE∥BD,CE⊥AC,且AE,CE相交于点E,求证:AD=CE.