题目内容
11.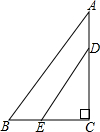 已知,在Rt△ABC中,∠C=90°,DE∥AB,AD=$\frac{1}{4}$AC,若CD=3,BE=$\frac{3}{4}$,求AB的长.
已知,在Rt△ABC中,∠C=90°,DE∥AB,AD=$\frac{1}{4}$AC,若CD=3,BE=$\frac{3}{4}$,求AB的长.
分析 先由AD=$\frac{1}{4}$AC可计算出AC=$\frac{4}{3}$CD=4,再根据平行线分线段成比例定理,由DE∥AB得$\frac{BE}{BC}$=$\frac{AD}{AC}$=$\frac{1}{4}$,则开始计算出BC=3,然后利用勾股定理可计算出AB.
解答 解:∵AD=$\frac{1}{4}$AC,
∴AC=4AD=4(AC-CD),
∴AC=$\frac{4}{3}$CD=$\frac{4}{3}$×3=4,
∵DE∥AB,
∴$\frac{BE}{BC}$=$\frac{AD}{AC}$,即$\frac{\frac{3}{4}}{BC}$=$\frac{1}{4}$,
∴BC=3,
在Rt△ABC中,AB=$\sqrt{B{C}^{2}+A{C}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5.
点评 本题考查了平行线分线段成比例:三条平行线截两条直线,所得的对应线段成比例.也考查了勾股定理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.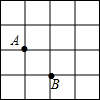 如图,A、B是边长为1的小正方形组成的网格上的两个格点,在格点中任意放置点C,恰好能使△ABC的面积为1的概率是( )
如图,A、B是边长为1的小正方形组成的网格上的两个格点,在格点中任意放置点C,恰好能使△ABC的面积为1的概率是( )
 如图,A、B是边长为1的小正方形组成的网格上的两个格点,在格点中任意放置点C,恰好能使△ABC的面积为1的概率是( )
如图,A、B是边长为1的小正方形组成的网格上的两个格点,在格点中任意放置点C,恰好能使△ABC的面积为1的概率是( )| A. | $\frac{6}{25}$ | B. | $\frac{1}{5}$ | C. | $\frac{4}{25}$ | D. | $\frac{7}{25}$ |
19.已知某同学近几次的数学成绩(单位:分)分别为92,90,88,92,93,则该同学这几次数学成绩的平均数和众数分别是( )
| A. | 90分,90分 | B. | 91分,92分 | C. | 92分,92分 | D. | 89分,92分 |
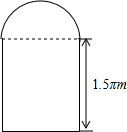 一条隧道的截面如图所示,它的上半部是一个半圆、下半部是一个矩形,矩形一边长为1.5πm,若隧道的截面积为5πm2.求半圆的半径(精确到0.01)
一条隧道的截面如图所示,它的上半部是一个半圆、下半部是一个矩形,矩形一边长为1.5πm,若隧道的截面积为5πm2.求半圆的半径(精确到0.01)