题目内容
有A、B两个布袋,A布袋中两个完全相同的小球,分别标有数字1和2,B布袋中有三个完全相同的小球,分别标有数字-2、0和3.小强从A布袋中随机取出一个小球,记录其标有的数字为a,再从B袋中随机取出一个小球,记录其标有的数字为b,这样就确定点P的一个坐标为(a,b)
(1)用列表或画树形图方法写出点P的所有可能坐标.
(2)求点P落在抛物线y=x2-3x+2上的概率.
(1)用列表或画树形图方法写出点P的所有可能坐标.
(2)求点P落在抛物线y=x2-3x+2上的概率.
考点:列表法与树状图法,二次函数图象上点的坐标特征
专题:计算题
分析:(1)利用树状图展示所有6种等可能的结果数,然后根据题意依次写出6个对应点的坐标;
(2)先计算出自变量为1和2所对应的函数值,再根据二次函数图象上点的坐标特征可判断点(1,0)和(2,0)在抛物线y=x2-3x+2上,然后根据概率公式计算点P落在抛物线y=x2-3x+2上的概率.
(2)先计算出自变量为1和2所对应的函数值,再根据二次函数图象上点的坐标特征可判断点(1,0)和(2,0)在抛物线y=x2-3x+2上,然后根据概率公式计算点P落在抛物线y=x2-3x+2上的概率.
解答:解:(1)画树状图为:

共有6种等可能的结果数,即点P的所有可能坐标为(1,-2),(1,0),(1,3),(2,-2),(2,0),(2,3);
(2)当x=1时,y=x2-3x+2=1-3+2=0;当x=2时,y=x2-3x+2=4-6+2=0,、
所以点(1,0)和(2,0)在抛物线y=x2-3x+2上,
所以点P落在抛物线y=x2-3x+2上的概率=
=
.

共有6种等可能的结果数,即点P的所有可能坐标为(1,-2),(1,0),(1,3),(2,-2),(2,0),(2,3);
(2)当x=1时,y=x2-3x+2=1-3+2=0;当x=2时,y=x2-3x+2=4-6+2=0,、
所以点(1,0)和(2,0)在抛物线y=x2-3x+2上,
所以点P落在抛物线y=x2-3x+2上的概率=
| 2 |
| 6 |
| 1 |
| 3 |
点评:本题考查了列表法与画树状图法:利用列表法或画树状图法展示所有可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后利用概率公式求解.也考查了二次函数图象上点的坐标特征.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案
相关题目
若实数x、y、z满足(x-z)2-4(x-y)(y-z)=0,则下列式子一定成立的是( )
| A、x+y=z |
| B、x+z=y |
| C、x+z=2y |
| D、x+y=2z |
已知二次函数y=ax2+bx+c的x、y的部分对应值如表:则该二次函数图象的对称轴为( )
| x | -1 | 0 | 1 | 2 | 3 |
| y | 5 | 1 | -1 | -1 | 1 |
| A、y轴 | ||
B、直线x=
| ||
| C、直线x=2 | ||
| D、直线x=2 |
已知函数y=2x2-16x+33的图象经过y=2x2的图象平移得到的,那么平移的过程可能是( )
| A、先向右平移4个单位,再向下平移1个单位 |
| B、先向右平移4个单位,再向上平移1个单位 |
| C、先向左平移4个单位,再向下平移1个单位 |
| D、先向左平移4个单位,再向上平移1个单位 |
如果m的相反数是-1,则(-m)2014-(-m)2015的值是( )
| A、4029 | B、2 |
| C、0 | D、2015 |
 二次函数y=ax2+bx+c的图象如图所示,则下列结论正确的是( )
二次函数y=ax2+bx+c的图象如图所示,则下列结论正确的是( )| A、c<0 | B、b>0 |
| C、b-2a=0 | D、a+b+c>0 |
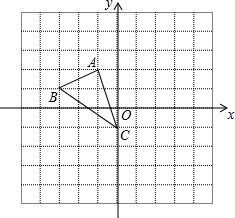 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(0,-1),
如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(0,-1), 如图,M为⊙O内一点,利用尺规作一条弦AB,使AB过点M,且AM=BM.
如图,M为⊙O内一点,利用尺规作一条弦AB,使AB过点M,且AM=BM.