题目内容
11.计算:($\frac{1}{2}$×$\frac{3}{2}$)×($\frac{2}{3}×\frac{4}{3}$)×($\frac{3}{4}×\frac{5}{4}$)×…×($\frac{2013}{2014}×\frac{2015}{2014}$)×($\frac{2014}{2015}×\frac{2016}{2015}$).分析 先去括号,再根据有理数的乘法,即可解答.
解答 解:原式=$\frac{1}{2}×\frac{3}{2}×\frac{2}{3}×\frac{4}{3}×\frac{3}{4}×\frac{5}{4}×…×\frac{2013}{2014}×\frac{2015}{2014}$×$\frac{2014}{2015}×\frac{2016}{2015}$
=$\frac{1}{2}×\frac{2016}{2015}$
=$\frac{1008}{2015}$.
点评 本题考查了有理数的乘法,解决本题的关键是进行约分.

练习册系列答案
相关题目
5.如图,图(1)是一个扇形AOB,将其作如下划分:第一次划分:如图(2)所示,得到扇形的总数为6个,分别为:扇形AOB、扇形AOC、扇形COB、扇形A1OB1、扇形A1OC1、扇形C1OB;第二次划分:如图(3)所示,在扇形C1OB1中,按上述划分方式继续划分,可以得到扇形的总数为11个;第三次划分:如图(4)所示;
依次划分下

(1)根据题意,完成表格
(2)请判断,按上述方式继续划分,能否得到扇形的总数为2000个?为什么?
依次划分下

(1)根据题意,完成表格
| 划分次数 | 扇形总个数 |
| 1 | 6 |
| 2 | 11 |
| 3 | 16 |
| 4 | 21 |
| … | … |
| n | 5n+1 |
 如图,在⊙O中,弦AB、CD相交于点E,∠BAC=40°,∠AED=75°,求∠ABD的度数.
如图,在⊙O中,弦AB、CD相交于点E,∠BAC=40°,∠AED=75°,求∠ABD的度数.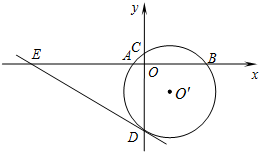 如图,已知⊙O′与x轴交于A、B两点,与y轴交于C、D两点,圆心O′的坐标是(1,-1),半径为$\sqrt{5}$.
如图,已知⊙O′与x轴交于A、B两点,与y轴交于C、D两点,圆心O′的坐标是(1,-1),半径为$\sqrt{5}$.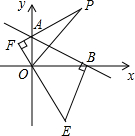 如图,直线y=-$\frac{1}{2}$x+2与坐标轴于A、B两点,BE⊥AB,BE=AB,AF⊥OE,垂足为F点
如图,直线y=-$\frac{1}{2}$x+2与坐标轴于A、B两点,BE⊥AB,BE=AB,AF⊥OE,垂足为F点