题目内容
1. 如图,在平面直角坐标系xOy中,已知点A(2,1)和点B(3,0),则sin∠AOB的值等于( )
如图,在平面直角坐标系xOy中,已知点A(2,1)和点B(3,0),则sin∠AOB的值等于( )| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{\sqrt{5}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{1}{2}$ |
分析 过A作AC垂直于x轴,由A的坐标确定出AC与OC的长,在直角三角形AOC中,利用勾股定理求出OA的长,再利用锐角三角函数定义求出所求即可.
解答  解:过A作AC⊥x轴,
解:过A作AC⊥x轴,
∵A(2,1),
∴AC=1,OC=2,
在Rt△AOC中,根据勾股定理得:OA=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,
则sin∠AOB=$\frac{AC}{OA}$=$\frac{\sqrt{5}}{5}$,
故选A
点评 此题考查了解直角三角形,坐标与图形性质,熟练掌握勾股定理及锐角三角函数定义是解本题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
9.-$\frac{3}{4}$的倒数是( )
| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | -$\frac{4}{3}$ | D. | -$\frac{3}{4}$ |
6.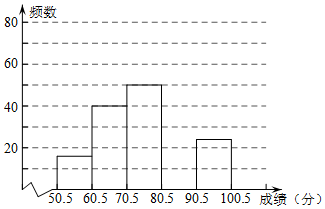 2015年3月30日是全国中小学生安全教育日,某学校为加强学生的安全意识,组织了全校1500名学生参加安全知识竞赛,从中抽取了部分学生成绩(得分取正整数,满分为100分)进行统计.请根据尚未完成的频率分布表和频数分布直方图,解答下列问题:
2015年3月30日是全国中小学生安全教育日,某学校为加强学生的安全意识,组织了全校1500名学生参加安全知识竞赛,从中抽取了部分学生成绩(得分取正整数,满分为100分)进行统计.请根据尚未完成的频率分布表和频数分布直方图,解答下列问题:
频率分布表
(1)这次抽取了200名学生的竞赛成绩进行统计,其中:m=70,n=0.12;
(2)补全频数分布直方图;
(3)若成绩在70分以下(含70分)的学生为安全意识不强,有待进一步加强安全教育,则该校安全意识不强的学生约有多少人?
 2015年3月30日是全国中小学生安全教育日,某学校为加强学生的安全意识,组织了全校1500名学生参加安全知识竞赛,从中抽取了部分学生成绩(得分取正整数,满分为100分)进行统计.请根据尚未完成的频率分布表和频数分布直方图,解答下列问题:
2015年3月30日是全国中小学生安全教育日,某学校为加强学生的安全意识,组织了全校1500名学生参加安全知识竞赛,从中抽取了部分学生成绩(得分取正整数,满分为100分)进行统计.请根据尚未完成的频率分布表和频数分布直方图,解答下列问题:频率分布表
| 分数段 | 频数 | 频率 |
| 50.5~60.5 | 16 | 0.08 |
| 60.5~70.5 | 40 | 0.2 |
| 70.5~80.5 | 50 | 0.25 |
| 80.5~90.5 | m | 0.35 |
| 90.5~100.5 | 24 | n |
(2)补全频数分布直方图;
(3)若成绩在70分以下(含70分)的学生为安全意识不强,有待进一步加强安全教育,则该校安全意识不强的学生约有多少人?
13. 如图,AB是⊙O的直径,A,C,D在圆上,∠D=65°,则∠ABC的度数为( )
如图,AB是⊙O的直径,A,C,D在圆上,∠D=65°,则∠ABC的度数为( )
 如图,AB是⊙O的直径,A,C,D在圆上,∠D=65°,则∠ABC的度数为( )
如图,AB是⊙O的直径,A,C,D在圆上,∠D=65°,则∠ABC的度数为( )| A. | 20° | B. | 25° | C. | 30° | D. | 35° |
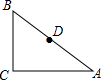 如图,在△ABC中,∠C=90°,AC=8,BC=6,D是边AB的中点,现有一点P位于边AC上,使得△ADP与△ABC相似,则线段AP的长为4或$\frac{25}{4}$.
如图,在△ABC中,∠C=90°,AC=8,BC=6,D是边AB的中点,现有一点P位于边AC上,使得△ADP与△ABC相似,则线段AP的长为4或$\frac{25}{4}$. 如图,直线y=-x+3与y轴交于点A,与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于点C,过点C作CB⊥x轴于点B,AO:BO=3,则反比例函数的解析式为y=-$\frac{4}{x}$.
如图,直线y=-x+3与y轴交于点A,与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于点C,过点C作CB⊥x轴于点B,AO:BO=3,则反比例函数的解析式为y=-$\frac{4}{x}$.