题目内容
10.已知x=$\frac{1}{2+\sqrt{3}}$,y=$\frac{1}{2-\sqrt{3}}$(1)求x2-3xy+y2的值;
(2)若x的整数部分是a,y的小数部分是b,求a2+b2的值.
分析 (1)先把x,y化简,再代入代数式计算;
(2)先估算$\sqrt{3}$的大小,再确定a,b的值,即可解答.
解答 解:x=$\frac{1}{2+\sqrt{3}}=\frac{2-\sqrt{3}}{(2+\sqrt{3})(2-\sqrt{3})}$=2-$\sqrt{3}$,y=$\frac{1}{2-\sqrt{3}}=\frac{2+\sqrt{3}}{(2-\sqrt{3})(2+\sqrt{3})}$=2+$\sqrt{3}$,
(1)x2-3xy+y2=$(2-\sqrt{3})^{2}-3(2+\sqrt{3})×(2-\sqrt{3})+(2+\sqrt{3})^{2}$
=7-4$\sqrt{3}$-3+7+4$\sqrt{3}$
=11.
(2)∵x=2-$\sqrt{3}$,y=2+$\sqrt{3}$,1<$\sqrt{3}$<2,
∴0<2-$\sqrt{3}$<1,3<2+$\sqrt{3}$<4,
∴x的整数部分是a=0,y的小数部分是b=2+$\sqrt{3}$-3=$\sqrt{3}$-1,
∴${a}^{2}+{b}^{2}={0}^{2}+(\sqrt{3}-1)^{2}$=4-2$\sqrt{3}$.
点评 本题考查了估算有理数的大小,解决本题的关键是估算$\sqrt{3}$的大小.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
1. 如图,在平面直角坐标系xOy中,已知点A(2,1)和点B(3,0),则sin∠AOB的值等于( )
如图,在平面直角坐标系xOy中,已知点A(2,1)和点B(3,0),则sin∠AOB的值等于( )
 如图,在平面直角坐标系xOy中,已知点A(2,1)和点B(3,0),则sin∠AOB的值等于( )
如图,在平面直角坐标系xOy中,已知点A(2,1)和点B(3,0),则sin∠AOB的值等于( )| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{\sqrt{5}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{1}{2}$ |
5.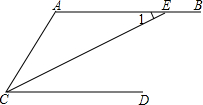 已知AB∥CD,CE平分∠ACD,交AB于点E,∠1=28°,则∠A的度数为( )
已知AB∥CD,CE平分∠ACD,交AB于点E,∠1=28°,则∠A的度数为( )
 已知AB∥CD,CE平分∠ACD,交AB于点E,∠1=28°,则∠A的度数为( )
已知AB∥CD,CE平分∠ACD,交AB于点E,∠1=28°,则∠A的度数为( )| A. | 56° | B. | 62° | C. | 118° | D. | 124° |
4.下列说法正确的有( )
| A. | a一定是正数 | B. | $\frac{7}{3}$是有理数 | ||
| C. | 0.5不是有理数 | D. | 平方等于自身的数只有1个 |
2.-3的相反数是( )
| A. | -3 | B. | -$\frac{1}{3}$ | C. | 3 | D. | $\frac{1}{3}$ |