Question

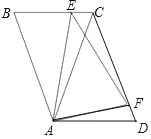
【题目】如图，在平行四边形ABCD中，AC＝CD．点E、F分别为边BC、CD上的两点，且∠EAF＝∠CAD

（1）求证：∠D＝∠ACB：

（2）求证：△ADF∽△ACE：

（3）求证：AE＝EF．

Answer 1

【答案】（1）证明见解析；（2）证明见解析；（3）证明见解析.

【解析】

（1）根据平行四边形性质得出∠ACB＝∠CAD，再利用等边对等角可以得到∠D＝∠CAD，进一步得出证明；

（2）根据两组角对应相等的两个三角形相等证明相似即可；

（3）根据△ADF∽△ACE得出对应边成比例，然后进一步证明△EAF∽△CAD，所以∠EFA＝∠D，最后进一步证明即可.

证明：（1）∵AC＝CD，

∴∠D＝∠CAD，

∵四边形ABCD为平行四边形，

∴BC∥AD，

∴∠ACB＝∠CAD，

∴∠D＝∠ACB；

（2）∵∠EAF＝∠CAD，

∴∠EAC＝∠DAF，

又∵∠D＝∠ACB，

∴△ADF∽△ACE：

（3）∵△ADF∽△ACE，

∴AD：AC＝AF：AE，

∴AD：AF＝AC：AE，

∵∠EAF＝∠CAD，

∴△EAF∽△CAD，

∴∠EFA＝∠D，

∴∠EAF＝∠EFA，

∴EA＝EF．