题目内容
12.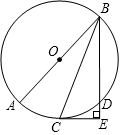 如图,已知AB为⊙O的直径,BC是弦,过C点的切线CE与弦BD的延长线相交于点E,且CE⊥BE,求证:$\widehat{AC}$=$\widehat{CD}$.
如图,已知AB为⊙O的直径,BC是弦,过C点的切线CE与弦BD的延长线相交于点E,且CE⊥BE,求证:$\widehat{AC}$=$\widehat{CD}$.
分析 作半径OC、OD,根据切线性质得:OC⊥CE,则OC∥BE,根据平行线的性质得同位角相等和内错角相等,再由同圆的半径相等,证得所对的角相等,则∠AOC=∠COD,从而$\widehat{AC}$=$\widehat{CD}$.
解答 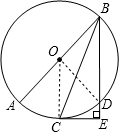 证明:连接OC、OD,
证明:连接OC、OD,
∵CE是⊙O的切线,
∴OC⊥CE,
∵CE⊥BE,
∴OC∥BE,
∴∠AOC=∠ABE,∠COD=∠ODB,
∵OB=OD,
∴∠ABE=∠ODB,
∴∠AOC=∠COD,
∴$\widehat{AC}$=$\widehat{CD}$.
点评 本题考查了切线的性质和与圆的关系的圆心角、弦、弧的性质,明确圆的切线垂直于过切点的半径,经常运用:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.在圆的证明题中,常作的辅助线有:①作半径,如本题,②作直径,③作弦心距等;

练习册系列答案
相关题目
8.若a+b=-1,则a2+b2+2ab的值为( )
| A. | 1 | B. | -1 | C. | 3 | D. | -3 |
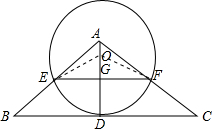 如图,在△ABC中,D为边BC的中点,O是AD上一点,⊙O与BC相切于点D,且与AB、AC分别相交于点E、F,连接EF交AD于点G.
如图,在△ABC中,D为边BC的中点,O是AD上一点,⊙O与BC相切于点D,且与AB、AC分别相交于点E、F,连接EF交AD于点G.