Question

7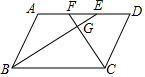．如图，在平行四边形ABCD中，BE，CF分别是∠ABC，∠BCD的平分线，BE，CF分别交边AD于点E，F，在平行四边形内部交于点G，设$\frac{BG}{EG}$=x，$\frac{AB}{BC}$=y，则y与x的函数表达式为y=$\frac{1+x}{2x}$．

Answer 1

分析 作辅助线，构建平行线，根据平行相似得：△EHG∽△EAB和△EGF∽△BGC，列比例式表示BC和AB的长，代入y式中，可求得y与x的函数表达式．

解答 解：过G作GH∥AB，交AD于H，
∵四边形ABCD是平行四边形，
∴AD∥BC，
∵BE，CF分别是∠ABC，∠BCD的平分线，
∴∠ABE=∠GBC=$\frac{1}{2}∠ABC$，∠GCB=$\frac{1}{2}∠BCD$，
∵AD∥BC，
∴∠AEB=∠GBC，
∴∠ABE=∠AEB，
∵GH∥AB，
∴△EHG∽△EAB，
∴$\frac{GH}{AB}=\frac{EG}{BE}$，
∵$\frac{BG}{EG}$=x，
∴$\frac{EG}{BE}=\frac{1}{1+x}$，
∴$\frac{GH}{AB}=\frac{1}{1+x}$，
∴AB=GH（1+x），
∵EF∥BC，
∴△EGF∽△BGC，
∴$\frac{EG}{BG}=\frac{EF}{BC}$，
∴$\frac{BC}{EF}=x$，
∴BC=EFx，
∴y=$\frac{GH（1+x）}{EFx}$，
∵GH∥AB，
∴∠ABE=∠HGE，
∴∠HGE=∠AEB，
∴GH=HE，
同理得：FH=GH，
∴GH=FH=HE，
∴$\frac{GH}{EF}$=$\frac{1}{2}$，
∴y=$\frac{1+x}{2x}$；
故答案为：y=$\frac{1+x}{2x}$．

点评 本题考查了相似三角形的性质和判定、平行四边形的性质，相似三角形常用的判定方法是：平行于三角形一边的直线，所构成的三角形与原三角形相似；相似三角形中一般辅助线作法是：通过作平行线构造相似三角形，使问题得以解决．