题目内容
如图，在Rt△ABC中，∠C=90°，D是AC边上一点，DE⊥AB于E，DE：AE=1：2．求sinB，cosB，tanB．考点：解直角三角形
专题：
分析：首先判断△ABC∽△ADE，则可得BC：AC=DE：AE=1：2，设BC=x，则AC=2x，求出AB后，即可求出sinB，cosB，tanB．
解答：解：∵∠A=∠A，∠AED=∠ACB，
∴△ABC∽△ADE，
∴BC：AC=DE：AE=1：2，
设BC=x，则AC=2x，
则AB=
=
x，
∴sinB=
=
，cosB=
=
x，tanB=
=2．
∴△ABC∽△ADE，
∴BC：AC=DE：AE=1：2，
设BC=x，则AC=2x，
则AB=
| BC2+AC2 |
| 5 |
∴sinB=
| AC |
| AB |
2
| ||
| 5 |
| BC |
| AB |
| ||
| 5 |
| AC |
| BC |
点评：本题考查了解直角三角形的知识，解答本题的关键是掌握相似三角形的判定与性质，及锐角三角函数的定义．
练习册系列答案
相关题目
如图所示，△ABC中，∠C=90°，AM平分∠CAB，BC=16cm，CM：MB=3：5，求点M到AB的距离．
在矩形ABCD中，对角线AC与BD相交于点O，∠ACB=30°，BD=4，求矩形ABCD的面积．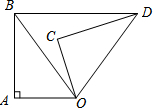
如图，在△OAB中，∠A=90°，△OCD是把△OAB以O为旋转中心，顺时针旋转而得到的（其中C与A对应），记旋转角为α，∠OBA为β．