题目内容
7.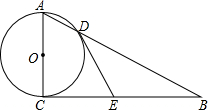 如图中,以AC为直径的⊙O交Rt△ABC的斜边AB于D,⊙O的切线DE交BC于E,求证:BE=CE.
如图中,以AC为直径的⊙O交Rt△ABC的斜边AB于D,⊙O的切线DE交BC于E,求证:BE=CE.
分析 连接CD,先证明∠CDB=90°,然后由切线长定理得到DE=EC,接下来在证明∠EDB=∠B,从而得到DE=EB,故此可证得BE=CE.
解答 证明:连接CD.
∵AC是圆O的直径,
∴∠ADC=90°.
∴∠CDB=90°.
∵∠ACB=90°,
∴BC是圆O的切线.
又∵DE是圆O的切线,
∴DE=EC.
∴∠EDC=∠ECD.
又∵∠CDE+∠EDB=90°,∠DCB+∠B=90°,
∴∠B=EDB.
∴EB=DE.
∴BE=CE.
点评 本题主要考查的是切线的性质、切线长定理、切线的判定,证得CE=ED=EB是解得关键.

练习册系列答案
相关题目
16. 一辆装满货物,宽为2.4米的卡车,欲通过如图的隧道,则卡车的外形高必须低于( )
一辆装满货物,宽为2.4米的卡车,欲通过如图的隧道,则卡车的外形高必须低于( )
 一辆装满货物,宽为2.4米的卡车,欲通过如图的隧道,则卡车的外形高必须低于( )
一辆装满货物,宽为2.4米的卡车,欲通过如图的隧道,则卡车的外形高必须低于( )| A. | 4.1米 | B. | 4.0米 | C. | 3.9米 | D. | 3.8米 |
 如图,可以用一个大写字母表示的角是∠A,以点B为顶点的角(小于平角)有∠EBA、∠EBD、∠ABD、∠ABF、∠DBF.
如图,可以用一个大写字母表示的角是∠A,以点B为顶点的角(小于平角)有∠EBA、∠EBD、∠ABD、∠ABF、∠DBF.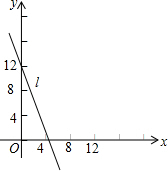 如图,直线l是一次函数y=kx+b的图象,观察图象可知:
如图,直线l是一次函数y=kx+b的图象,观察图象可知: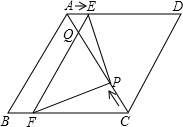 如图,在?ABCD中,AB=6cm,AD=AC=5cm,点P由C出发沿CA方向匀速运动,速度为1cm/s,同时,线段EF由AB出发沿AD方向匀速运动,速度为1cm/s,交AC于Q,连接PE、PF,若设运动时间为t(s)(0<t<5),解答下列问题:
如图,在?ABCD中,AB=6cm,AD=AC=5cm,点P由C出发沿CA方向匀速运动,速度为1cm/s,同时,线段EF由AB出发沿AD方向匀速运动,速度为1cm/s,交AC于Q,连接PE、PF,若设运动时间为t(s)(0<t<5),解答下列问题: