题目内容
9.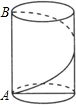 如图为一圆柱体工艺品,其底面周长为60cm,高为25cm,从点A出发绕该工艺品侧面一周镶嵌一根装饰线到点B,则该装饰线最短长为65cm.
如图为一圆柱体工艺品,其底面周长为60cm,高为25cm,从点A出发绕该工艺品侧面一周镶嵌一根装饰线到点B,则该装饰线最短长为65cm.
分析 将圆柱的侧面展开,得到一个长方体,然后利用两点之间线段最短可得AB′的长即是装饰线的最短路线长,然后由勾股定理求解即可.
解答 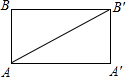 解:沿AB剪开可得矩形,如图所示:
解:沿AB剪开可得矩形,如图所示:
∵圆柱的高为25cm,底面圆的周长为60cm,
∴A′B′=AB=25cm,AA′=60cm,
在Rt△AA′B′中,AB′=$\sqrt{A′{A}^{2}+A′B{′}^{2}}$=65(cm),
即装饰线的最短路线长是:65cm.
故答案为:65.
点评 本题考查了平面展开---最短路径问题,解题的关键是会将圆柱的侧面展开,并利用勾股定理解答.

练习册系列答案
相关题目
14.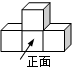 如图,由4个正方体组成的几何体的左视图是( )
如图,由4个正方体组成的几何体的左视图是( )
 如图,由4个正方体组成的几何体的左视图是( )
如图,由4个正方体组成的几何体的左视图是( )| A. | 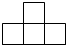 | B. |  | C. |  | D. | 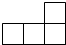 |
1.-$\frac{2}{3}$的相反数是( )
| A. | $\frac{2}{3}$ | B. | -$\frac{3}{2}$ | C. | $\frac{3}{2}$ | D. | -$\frac{2}{3}$ |
19.若x2-2(k-1)x+4是完全平方式,则k的值为( )
| A. | ±1 | B. | ±3 | C. | 1或-3 | D. | -1或3 |
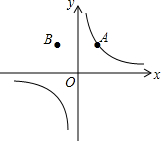 如图,已知点A和B(-1,2)关于y轴对称,反比例函数$y=\frac{k}{x}$的图象经过点A,则k的值为2.
如图,已知点A和B(-1,2)关于y轴对称,反比例函数$y=\frac{k}{x}$的图象经过点A,则k的值为2.