题目内容
14.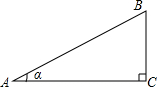 如图,定义:在直角三角形ABC中,锐角α的邻边与对边的比叫做角α的余切,记作cotα,即cotα=$\frac{角α的邻边}{角α的对边}$=$\frac{AC}{BC}$.根据上述角的余切定义,解下列问题:
如图,定义:在直角三角形ABC中,锐角α的邻边与对边的比叫做角α的余切,记作cotα,即cotα=$\frac{角α的邻边}{角α的对边}$=$\frac{AC}{BC}$.根据上述角的余切定义,解下列问题:(1)cot30°=$\sqrt{3}$;
(2)如图,已知tanA=$\frac{3}{4}$,其中∠A为锐角,试求cotA的值.
分析 (1)根据直角三角形的性质用BC表示出AB及AC的值,再根据锐角三角函数的定义进行解答即可;
(2)由于tanA=$\frac{BC}{AC}$=$\frac{3}{4}$,所以可设BC=3k,AC=4k,再根据锐角三角函数的定义进行解答即可.
解答 解:(1)∵Rt△ABC中,α=30°,
∴BC=$\frac{1}{2}$AB,即AB=2BC,
∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=$\sqrt{(2BC)^{2}-B{C}^{2}}$=$\sqrt{3}$BC,
∴cot30°=$\frac{AC}{BC}$=$\sqrt{3}$.
故答案为:$\sqrt{3}$;
(2)∵tanA=$\frac{BC}{AC}$=$\frac{3}{4}$,
∴设BC=3k,AC=4k,
∴cotA=$\frac{AC}{BC}$=$\frac{4k}{3k}$=$\frac{4}{3}$.
点评 本题考查的是锐角三角函数的定义及直角三角形的性质,熟知锐角三角函数的定义是解答此题的关键.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
4.在⊙O与⊙O′中,若∠AOB=∠A′O′B′,则AB与A′B′的关系为( )
| A. | AB=A′B′ | B. | AB>A′B′ | C. | AB<A′B′ | D. | 无法确定 |
5.小明沿着坡度为1:2的山坡向上走了1 000m,则他升高了( )
| A. | 200$\sqrt{5}$m | B. | 500m | C. | 500$\sqrt{3}$m | D. | 1000m |
2.△ABC中,tanA=1,cosB=$\frac{\sqrt{3}}{2}$,则△ABC为( )
| A. | 锐角三角形 | B. | 钝角三角形 | C. | 直角三角形 | D. | 不能确定 |
9.在Rt△ABC中,∠C=90°,tanA=$\frac{2}{3}$,AC=4,则BC等于( )
| A. | $\frac{8}{3}$ | B. | 2 | C. | 1 | D. | $\frac{7}{3}$ |
19.sin45°的值是( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |

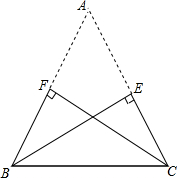 如图是缺了一个角的三角形纸片ABC,已知BE⊥AC,垂足为E,CF⊥AB,垂足为F,且BE=CF,请你根据以上条件判断△ABC的形状,并说明理由:
如图是缺了一个角的三角形纸片ABC,已知BE⊥AC,垂足为E,CF⊥AB,垂足为F,且BE=CF,请你根据以上条件判断△ABC的形状,并说明理由: