题目内容
17.计算:(1)$\sqrt{4.41}$;
(2)$\sqrt{1\frac{11}{25}}$;
(3)$\sqrt{1{7}^{2}-{15}^{2}}$.
分析 (1)根据二次根式的性质化简即可;
(2)根据二次根式的性质化简即可;
(3)先根据平方差公式计算,然后根据二次根式的性质化简即可.
解答 解:(1)$\sqrt{4.41}$=$\sqrt{\frac{441}{100}}$=$\frac{21}{10}$;
(2)$\sqrt{1\frac{11}{25}}$=$\sqrt{\frac{36}{25}}$=$\frac{6}{5}$;
(3)$\sqrt{1{7}^{2}-{15}^{2}}$=$\sqrt{(17+15)(17-15)}$=$\sqrt{64}$=8.
点评 本题考查了二次根式的化简和化简,解答此题,要弄清以下问题:
①定义:一般地,形如$\sqrt{a}$(a≥0)的代数式叫做二次根式.当a>0时,$\sqrt{a}$表示a的算术平方根;当a=0时,$\sqrt{0}$=0;当a<0时,非二次根式(在一元二次方程中,若根号下为负数,则无实数根).
②性质:$\sqrt{{a}^{2}}$=|a|.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.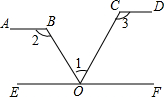 如图,AB∥CD∥EF,下列各式中,正确的是( )
如图,AB∥CD∥EF,下列各式中,正确的是( )
 如图,AB∥CD∥EF,下列各式中,正确的是( )
如图,AB∥CD∥EF,下列各式中,正确的是( )| A. | ∠1+∠2+∠3=180° | B. | ∠1+∠2-∠3=90° | C. | ∠1-∠2+∠3=90° | D. | ∠2+∠3-∠1=180° |
 将长方形ABCD沿AE折叠,得到如图所示的图形,已知∠CEB′=$\frac{2}{5}$∠AEB′,则∠AEB′=75°.
将长方形ABCD沿AE折叠,得到如图所示的图形,已知∠CEB′=$\frac{2}{5}$∠AEB′,则∠AEB′=75°. 如图,当∠1=∠3时,AB∥CD.
如图,当∠1=∠3时,AB∥CD.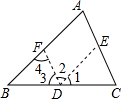 已知:△ABC,求证:∠A+∠B+∠C=180°.(证明方法有多种)小明的证法如下:(请你将小明的证法补充完整,并在括号内填入推理的根据)
已知:△ABC,求证:∠A+∠B+∠C=180°.(证明方法有多种)小明的证法如下:(请你将小明的证法补充完整,并在括号内填入推理的根据)