题目内容
16.计算:(1)($\sqrt{72}$+$\frac{1}{2}\sqrt{6}$)÷$\sqrt{8}$ (2)(3$\sqrt{2}$$+5\sqrt{3}$)2
(3)4$\sqrt{5}$$-\sqrt{8}$($\sqrt{45}$-4$\sqrt{2}$) (4)(2$\sqrt{7}$+5)(2$\sqrt{7}$-5)
分析 (1)首先化简二次根式,进而利用二次根式除法运算法则得出答案;
(2)直接利用完全平方公式得出答案;
(3)首先化简二次根式,进而利用二次根式乘法运算法则得出答案;
(4)直接利用平方差公式计算得出答案.
解答 解:(1)($\sqrt{72}$+$\frac{1}{2}\sqrt{6}$)÷$\sqrt{8}$
=(6$\sqrt{2}$+$\frac{\sqrt{6}}{2}$)×$\frac{1}{2\sqrt{2}}$
=3+$\frac{\sqrt{3}}{4}$;
(2)(3$\sqrt{2}$$+5\sqrt{3}$)2=18+75+30$\sqrt{6}$=93+30$\sqrt{6}$;
(3)4$\sqrt{5}$$-\sqrt{8}$($\sqrt{45}$-4$\sqrt{2}$)
=4$\sqrt{5}$-2$\sqrt{2}$(3$\sqrt{5}$-4$\sqrt{2}$)
=4$\sqrt{5}$-6$\sqrt{10}$+16;
(4)(2$\sqrt{7}$+5)(2$\sqrt{7}$-5)
=28-25
=3.
点评 此题主要考查了二次根式的混合运算,正确化简二次根式是解题关键.

练习册系列答案
相关题目
6.函数y=$\sqrt{x+1}$中自变量x的取值范围是( )
| A. | x≥0 | B. | x>-1 | C. | x≥-1 | D. | x≥1 |
1.已知△ABC的三边长都是整数,且AB=2,BC=6,则△ABC的周长可能是( )
| A. | 12 | B. | 14 | C. | 16 | D. | 17 |
8.若多项式a2+kab+b2是完全平方式,则常数k的值为( )
| A. | 2 | B. | 4 | C. | ±2 | D. | ±4 |
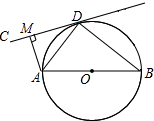 如图,AB为⊙O的直径,直线CD切⊙O于点D,AM⊥CD于点M,连接AD,BD.
如图,AB为⊙O的直径,直线CD切⊙O于点D,AM⊥CD于点M,连接AD,BD.