题目内容
13．如图，已知AB：BC：CD=2：3：4，E、F分别为AB、CD中点，且EF=15．求线段AD的长．
分析 根据题意可设AB=2x，然后根据图形列出方程即可求出AD的长度．
解答 解：设AB=2x，BC=3x，CD=4x，
∵E、F分别是AB和CD的中点，
∴BE=$\frac{1}{2}$AB=x，CF=$\frac{1}{2}$CD=2x，
∵EF=15cm，
∴BE+BC+CF=15cm，
∴x+3x+2x=15，
解得：x=$\frac{5}{2}$，
∴AD=AB+BC+CD=2x+3x+4x=9x=$\frac{45}{2}$cm
点评 本题考查线段相加减问题，涉及一元一次方程的解法．
练习册系列答案
相关题目
4．
如图所示，BD是△ABC的角平分线，DE垂直平分BC，若∠A=120°，则∠C的度数为（ ）
如图所示，BD是△ABC的角平分线，DE垂直平分BC，若∠A=120°，则∠C的度数为（ ）| A． | 15° | B． | 20° | C． | 25° | D． | 30° |
如图，⊙O与△ADE各边所在的直线分别相切于B、F、C，DE⊥AE，AD=10，AE=6．
8．
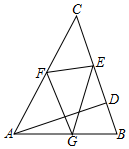△ABC中，∠BAC=60°，AD⊥BC于D，且AD=$\sqrt{3}$，E、F、G分别为边BC、CA、AB上的点，则△EFG周长的最小值为（ ）
△ABC中，∠BAC=60°，AD⊥BC于D，且AD=$\sqrt{3}$，E、F、G分别为边BC、CA、AB上的点，则△EFG周长的最小值为（ ）| A． | $\sqrt{3}$ | B． | 2$\sqrt{3}$ | C． | 3 | D． | 3$\sqrt{3}$ |
四边形ABCD中，∠ABC=∠ADC=90°，EF是BD的垂直平分线交AC于点F，求证：点F是AC的中点．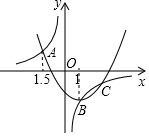
如图，二次函数y1=ax2+bx+c与反比例函数y2=$\frac{k}{x}$的图象交于A（-1.5，p），B（1，q），C（2.5，r）三点，则当y1＜y2时，x的取值范围是-1.5＜x＜0或1＜x＜2.5．
7．将（-a+b-1）（a+b+1）化为（m+n）（m-n）的形式为（ ）
| A． | [b+（a+1）][b-（a-1）] | B． | [b+（a+1）][b-（a+1）] | C． | [b+（a+1）][b-（-a+1）] | D． | [b+（a+1）][（b-a）-1]． |
