题目内容
如图,在矩形ABCD中,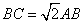 ,∠ADC的平分线交边BC于点E,AH⊥DE于点H,连接CH并延长交边AB于点F,连接AE交CF于点O,给出下列命题:
,∠ADC的平分线交边BC于点E,AH⊥DE于点H,连接CH并延长交边AB于点F,连接AE交CF于点O,给出下列命题:
①∠AEB=∠AEH ②DH=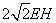 ③
③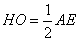 ④
④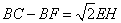
其中正确命题的序号是 (填上所有正确命题的序号).
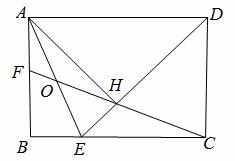
①③.
【考点】矩形的性质;等腰(直角)三角形的判定和性质;三角形内角和定理;全等三角形的判定和性质;直角三角形斜边上的中线的判定;勾股定理;相似三角形的判定和性质;特殊元素法和方程思想的应用.
【分析】①∵在矩形ABCD中,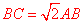 ,∴不妨设
,∴不妨设 ,则
,则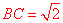 .
.
∵∠ADC的平分线交边BC于点E,∴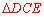 是等腰直角三角形.∴
是等腰直角三角形.∴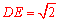 .
.
∴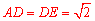 .∴
.∴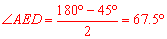 .
.
∴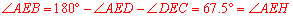 .故命题①正确.
.故命题①正确.
②∵ 是等腰直角三角形,∴
是等腰直角三角形,∴ .
.
∵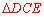 是等腰直角三角形,∴
是等腰直角三角形,∴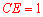 .∴
.∴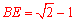 .
.
不难证明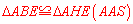 ,∴
,∴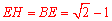 .∴
.∴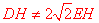 .故命题②错误.
.故命题②错误.
③∵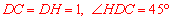 ,∴
,∴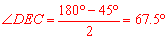 .∴
.∴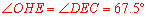 。
。
∵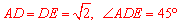 ,∴
,∴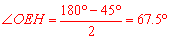 .
.
∴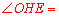
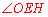 .∴
.∴ 是
是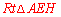 斜边上的中线.∴
斜边上的中线.∴ .故命题③正确.
.故命题③正确.
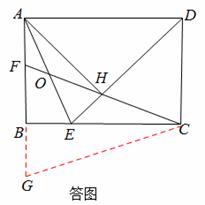 ④如答图,延长AB至G,使BG=BF,连接CG,
④如答图,延长AB至G,使BG=BF,连接CG,
在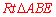 中,
中,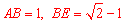 ,
,
∴根据勾股定理得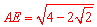 .
.
设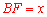 ,则
,则 .
.
在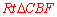 中,根据勾股定理得
中,根据勾股定理得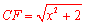 .
.
易证明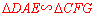 ,∴
,∴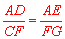 .
.
∴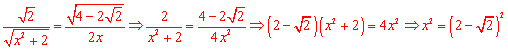 .
.
∴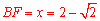 .
.
∴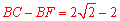 .
.
又∵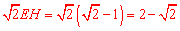 .
.
∴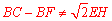 .故命题④错误.
.故命题④错误.
综上所述,正确命题的序号是①③.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目

 B.
B. C.
C. D.
D. 
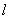 翻折后,点B落在边AC的中点E处,直线
翻折后,点B落在边AC的中点E处,直线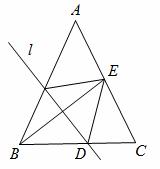
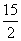 C.
C.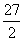 D.12
D.12 
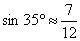 ,
, 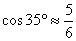 ,
,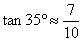
 ,则k的值是 ( )
,则k的值是 ( )