题目内容
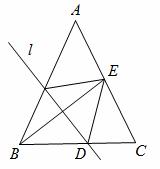
如图,在△ABC中,AB=AC,BC=24,tanC=2,如果将△ABC沿直线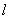 翻折后,点B落在边AC的中点E处,直线
翻折后,点B落在边AC的中点E处,直线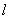 与边BC交于点D,那么BD的长为【 】
与边BC交于点D,那么BD的长为【 】
A.13 B.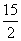 C.
C.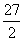 D.12
D.12
A.
 【考点】翻折问题;等腰三角形的性质;勾股定理;翻折对称的性质;锐角三角函数定义;方程思想的应用.
【考点】翻折问题;等腰三角形的性质;勾股定理;翻折对称的性质;锐角三角函数定义;方程思想的应用.
【分析】如答图,过点E作EH⊥BC于点H,
∵AB=AC,BC=24,∴CH=12.
∵tanC=2,∴AH=24.
∴根据勾股定理得 .
.
∵点E是边AC的中点,∴ .
.
设 ,则
,则 .
.
∵△ABC沿直线 翻折,点B落在边AC的中点E处,∴BD=DE
翻折,点B落在边AC的中点E处,∴BD=DE .
.
在 中,
中, .
.
在 中,
中, .
.
∴BD=DE .
.
故选A.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
 的不等式组的解集是
的不等式组的解集是
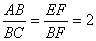 ,求
,求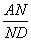 的值;
的值; ,当
,当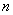 为何值时,MN∥BE?
为何值时,MN∥BE?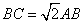 ,∠ADC的平分线交边BC于点E,AH⊥DE于点H,连接CH并延长交边AB于点F,连接AE交CF于点O,给出下列命题:
,∠ADC的平分线交边BC于点E,AH⊥DE于点H,连接CH并延长交边AB于点F,连接AE交CF于点O,给出下列命题: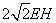 ③
③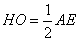 ④
④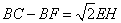
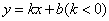 的图象经过点C(3,0),且与两坐标轴围成的三角形的面积为3.
的图象经过点C(3,0),且与两坐标轴围成的三角形的面积为3. 的图象与该一次函数的图象交于二、四象限内的A、B两点,且AC=2BC,求
的图象与该一次函数的图象交于二、四象限内的A、B两点,且AC=2BC,求 的值.
的值.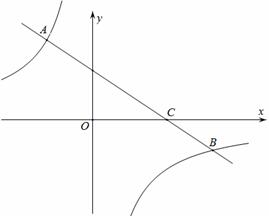
 ,直线
,直线 外一点A.
外一点A. ,垂足为C)斜边AB=c.
,垂足为C)斜边AB=c.
 B.
B. C.
C. D.
D.