题目内容
18.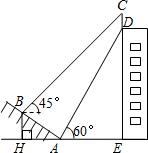 如图,某大楼的顶部竖有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡
如图,某大楼的顶部竖有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1:$\sqrt{3}$,AB=20米,AE=30米.
(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.
分析 (1)过B作DE的垂线,设垂足为G.分别在Rt△ABH中,通过解直角三角形求出BH、AH;
(2)在△ADE解直角三角形求出DE的长,进而可求出EH即BG的长,在Rt△CBG中,∠CBG=45°,则CG=BG,由此可求出CG的长然后根据CD=CG+GE-DE即可求出宣传牌的高度.
解答 解:(1)过B作BG⊥DE于G,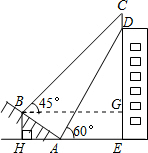
Rt△ABH中,i=tan∠BAH=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,
∴∠BAH=30°,
∴BH=$\frac{1}{2}$AB=10米;
(2)∵BH⊥HE,GE⊥HE,BG⊥DE,
∴四边形BHEG是矩形.
∵由(1)得:BH=10,AH=10$\sqrt{3}$米,
∴BG=AH+AE=(10$\sqrt{3}$+30)米,
Rt△BGC中,∠CBG=45°,
∴CG=BG=10$\sqrt{3}$+30.
Rt△ADE中,∠DAE=60°,AE=30米,
∴DE=$\sqrt{3}$AE=30$\sqrt{3}$米.
∴CD=CG+GE-DE=10$\sqrt{3}$+30+10-30$\sqrt{3}$=40-20$\sqrt{3}$(米).
答:宣传牌CD高约(40-20$\sqrt{3}$)米.
点评 此题综合考查了仰角、坡度的定义,能够正确地构建出直角三角形,将实际问题化归为解直角三角形的问题是解答此类题的关键.

练习册系列答案
相关题目
6. 实数a,b在数轴上的位置如图所示,下列结论中正确的是( )
实数a,b在数轴上的位置如图所示,下列结论中正确的是( )
 实数a,b在数轴上的位置如图所示,下列结论中正确的是( )
实数a,b在数轴上的位置如图所示,下列结论中正确的是( )| A. | a>b | B. | |a|>|b| | C. | -a<b | D. | a+b<0 |
13.下列汽车标志中国,是中心对称图形但不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
7. 如图,圆锥的表面展开图由一个扇形和一个圆组成,已知圆的面积为100π,扇形的圆心角为120°,则这个扇形的面积为( )
如图,圆锥的表面展开图由一个扇形和一个圆组成,已知圆的面积为100π,扇形的圆心角为120°,则这个扇形的面积为( )
 如图,圆锥的表面展开图由一个扇形和一个圆组成,已知圆的面积为100π,扇形的圆心角为120°,则这个扇形的面积为( )
如图,圆锥的表面展开图由一个扇形和一个圆组成,已知圆的面积为100π,扇形的圆心角为120°,则这个扇形的面积为( )| A. | 300π | B. | 150π | C. | 200π | D. | 600π |
8.据国家考试中心发布的信息,我国2007年参加高考的考生数达10 100 000人,这个数据用科学记数法可表示为( )
| A. | 0.101×108 | B. | 1.01×107 | C. | 10.1×106 | D. | 101×105 |
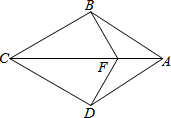 如图,在四边形ABCD中,AB=AD,CB=CD,点F是AC上一点,连结BF,DF.
如图,在四边形ABCD中,AB=AD,CB=CD,点F是AC上一点,连结BF,DF.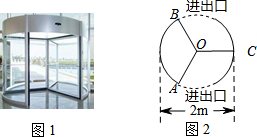 三翼式旋转门在圆柱形的空间内旋转,旋转内的三片旋转翼把空间等分成三个部分,如图1,旋转门的俯视图是直径的2米的圆,图2显示了某一时刻旋转翼的位置,则弧AB的长是$\frac{2}{3}$π米.(结果保留π)
三翼式旋转门在圆柱形的空间内旋转,旋转内的三片旋转翼把空间等分成三个部分,如图1,旋转门的俯视图是直径的2米的圆,图2显示了某一时刻旋转翼的位置,则弧AB的长是$\frac{2}{3}$π米.(结果保留π)