题目内容
13.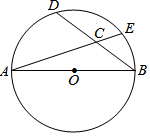 如图,AB是⊙O的直径,点D是弧AE的中点,AB=5,BD=4,则sin∠ECB=$\frac{4}{5}$.
如图,AB是⊙O的直径,点D是弧AE的中点,AB=5,BD=4,则sin∠ECB=$\frac{4}{5}$.
分析 作辅助线,根据直径所对的圆周角是直角,构建两个直角三角形,再利用弧的中点的定义及弧相等,则所对的圆周角相等得:∠ABD=∠CBE,根据等角的余角相等得:∠ECB=∠DAB,最后利用等角的三角函数得出结论.
解答  解:连接BE、AD,
解:连接BE、AD,
∵AB是⊙O的直径,
∴∠AEB=∠ADB=90°,
∴∠ECB+∠CBE=90°,∠ABD+∠DAB=90°,
∵D为$\widehat{AE}$的中点,
∴$\widehat{AD}$=$\widehat{DE}$,
∴∠ABD=∠CBE,
∴∠ECB=∠DAB,
在Rt△ADB中,∵BD=4,AB=5,
∴sin∠DAB=$\frac{BD}{AB}$=$\frac{4}{5}$,
∴sin∠ECB=$\frac{4}{5}$,
故答案为:$\frac{4}{5}$.
点评 本题考查了圆周角定理和解直角三角形,掌握圆周角的两个定理:①在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.②半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.这两个性质在圆的证明题中经常运用,要熟练掌握.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
18.在圆周长计算公式C=2πr中,对半径不同的圆,变量有( )
| A. | C,r | B. | C,π,r | C. | C,π | D. | C,2π,r |
5.方程2x2-3x+1=0化为(x+a)2=b的形式,正确的是( )
| A. | (x-$\frac{3}{2}$)2=16 | B. | 2(x-$\frac{3}{4}$)2=$\frac{1}{16}$ | C. | (x-$\frac{3}{4}$)2=$\frac{1}{16}$ | D. | 以上都不对 |
3.关于x的不等式x-b≥0恰有两个负整数解,则b的取值范围是( )
| A. | -3<b<-2 | B. | -3<b≤-2 | C. | -3≤b≤-2 | D. | -3≤b<-2 |
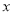 轴方向向左平移6个单位,画出平移后得到的△A1B1C1;
轴方向向左平移6个单位,画出平移后得到的△A1B1C1;