题目内容
10．
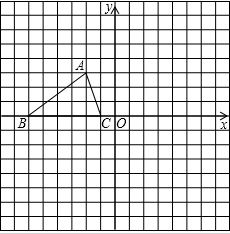如图所示，已知△ABC的三个顶点的坐标分别为A（-2，3），B（-6，0），C（-1，0）．（1）请直接写出点A关于原点O对称的点的坐标；
（2）将△ABC绕坐标原点O逆时针旋转90°，求A点经过的路径长；
（3）请直接写出：以A、B、C为顶点的平行四边形的第四个顶点D的坐标．
分析 （1）直接写出点A关于原点O对称的点的坐标即可．
（2）根据网格结构找出点A、B、C绕坐标原点O逆时针旋转90°对应点A′、B′、C′的位置，然后顺次连接即可，再根据平面直角坐标系写出点B′的坐标，根据弧长公式列式计算即可得解；
（3）根据平行四边形的对边平行且相等，分AB、BC、AC是对角线三种情况分别写出即可．
解答 
解：（1）点A关于原点O对称的点的坐标为（2，-3）；
（2）△ABC旋转后的△A′B′C′如图所示，
点A′的对应点的坐标为（-3，-2）；
OA′=$\sqrt{{3}^{2}+{2}^{2}}$=$\sqrt{13}$，
即点A所经过的路径长为$\frac{90π\sqrt{13}}{180}$=$\frac{\sqrt{13}}{2}π$；
（3）若AB是对角线，则点D（-7，3），
若BC是对角线，则点D（-5，-3），
若AC是对角线，则点D（3，3）．
点评 本题考查了利用旋转变换作图，平行四边形的对边平行且相等的性质，弧长公式，熟练掌握网格结构准确找出对应点的位置是解题的关键，难点在于（3）分情况讨论．
练习册系列答案
相关题目
如图，某数学兴趣小组在活动课上测量学校旗杆的高度．已知小亮站着测量，眼睛与地面的距离（AB）是1.7米，看旗杆顶部E的仰角为30°；小敏蹲着测量，眼睛与地面的距离（CD）是0.7米，看旗杆顶部E的仰角为45°．两人相距5米且位于旗杆同侧（点B、D、F在同一直线上）．
如图所示在直角梯形ABCD中，AD∥BC，∠A=90°，AB=12，BC=21，AD=16．动点P从点B出发，沿射线BC的方向以每秒2个单位长的速度运动，动点Q同时从点A出发，在线段AD上以每秒1个单位长的速度向点D运动，当其中一个动点到达端点时另一个动点也随之停止运动．设运动的时间为t（秒）．
如图，已知tan∠EOF=2，点C在射线OF上，OC=12．点M是∠EOF内一点，MC⊥OF于点C，CM=4．在射线CF上取一点A，连接AM并延长交射线OE于点B，作BD⊥OF于点D．