Question

8．如图，平面直角坐标系xOy中，点A、B的坐标分别为（3，0）、（2，-3），△AB′O′是△ABO关于点A的位似图形，且O′的坐标为（-1，0）．
（1）画出△AB′O′；
（2）求出点B′的坐标．

Answer 1

分析 （1）直接利用位似图形的性质得出对应点位置进而得出答案；
（2）利用位似图形的性质结合一次函数解析式求法以及一次函数图象上点的坐标特征进而得出答案．

解答 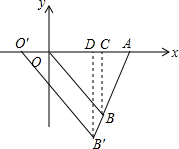解：（1）如图所示：△AB′O′即为所求；

（2）过点B作BC⊥OA于点C，过点B′作B′D⊥AO于点D，
∵△AB′O′是△ABO关于点A的位似图形，
∴$\frac{AO}{AO′}$=$\frac{BC}{B′D}$，
∴$\frac{3}{4}$=$\frac{3}{DB′}$，
解得：DB′=4，
设直线AB的解析式为：y=kx+b，
则$\left\{\begin{array}{l}{3k+b=0}\\{2k+b=-3}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{k=3}\\{b=-9}\end{array}\right.$，
故直线AB的解析式为：y=3x-9，
当y=-4时，-4=3x-9，
解得：x=$\frac{5}{3}$，
故B′点坐标为：（$\frac{5}{3}$，-4）．

点评 此题主要考查了位似变换以及位似图形的性质和待定系数法求一次函数解析式等知识，正确利用位似图形的性质得出对应点坐标是解题关键．