题目内容
11.如图1,已知△ABC中,AB=10cm,AC=8cm,BC=6cm,如果点P由B出发沿BA方向向点A匀速运动,同时点Q由A出发沿AC方向向点C匀速运动,它们的速度均为2cm/s,连接PQ,设运动的时间为t(单位:s)(0≤t≤4).解答下列问题:
(1)当t为何值时,PQ∥BC.
(2)是否存在某时刻t,使线段PQ恰好把△ABC的面积平分?若存在求出此时t的值;若不存在,请说明理由.
(3)如图2,把△APQ沿AP翻折,得到四边形AQPQ′.那么是否存在某时刻t使四边形AQPQ′为菱形?若存在,求出此时菱形的面积;若不存在,请说明理由.
分析 (1)根据PQ∥BC,得出△APQ∽△ABC,根据相似三角形对应边成比例,列出比例式,求出方程的解即可;
(2)假设存在某时刻t,使线段PQ恰好把△ABC的面积平分,据此得出一元二次方程;由于此一元二次方程的判别式小于0,则可以得出结论:不存在这样的某时刻t,使线段PQ恰好把△ABC的面积平分;
(3)首先根据菱形的性质及相似三角形比例线段关系,求得PQ、QD和PD的长度;然后在Rt△PQD中,根据勾股定理列出方程(8-$\frac{18}{5}$t)2+(6-$\frac{6}{5}$t)2=(2t)2,求得时间t的值;最后根据菱形的面积等于△AQP面积的2倍,进行计算即可.
解答 解:(1)由题意知:BP=2t,AP=10-2t,AQ=2t,
∵PQ∥BC,
∴△APQ∽△ABC,
∴$\frac{AP}{AB}$=$\frac{AQ}{AC}$,
即$\frac{10-2t}{10}$=$\frac{2t}{8}$,
解得:t=$\frac{20}{9}$,
∴当t=$\frac{20}{9}$时,PQ∥BC;
(2)如图1所示,过P点作PD⊥AC于点D,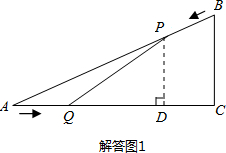
∴PD∥BC,
∴$\frac{AP}{AB}$=$\frac{PD}{BC}$,即$\frac{10-2t}{10}$=$\frac{PD}{6}$,
解得$PD=6-\frac{6}{5}t$,
∴△AQP的面积$S=\frac{1}{2}PD×AQ=6t-\frac{6}{5}{t^2}$,
假设存在某时刻t,使线段PQ恰好把△ABC的面积平分,
则有S△AQP=$\frac{1}{2}$S△ABC,
∵△ABC中,AB=10cm,AC=8cm,BC=6cm,
∴△ABC是直角三角形,且∠C=90°,
∴S△ABC=$\frac{1}{2}$AC•BC=24,
∴S△AQP=12,
而S△AQP=$6t-\frac{6}{5}{t^2}$,
∴$6t-\frac{6}{5}{t^2}=12$,
化简得:t2-5t+10=0,
∵△=(-5)2-4×1×10=-15<0,
∴此方程无解,
∴不存在某时刻t,使线段PQ恰好把△ABC的面积平分;
(3)假设存在时刻t,使四边形AQPQ′为菱形,则有AQ=PQ=BP=2t.
如图2所示,过P点作PD⊥AC于点D,则有PD∥BC,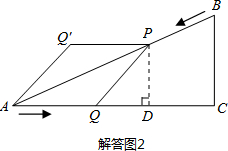
∴$\frac{AD}{AC}$=$\frac{AP}{AB}$=$\frac{PD}{BC}$,
即$\frac{AD}{8}$=$\frac{10-2t}{10}$=$\frac{PD}{6}$,
解得:PD=6-$\frac{6}{5}$t,AD=8-$\frac{8}{5}$t,
∴QD=AD-AQ=8-$\frac{8}{5}$t-2t=8-$\frac{18}{5}$t,
在Rt△PQD中,由勾股定理得:QD2+PD2=PQ2,
即(8-$\frac{18}{5}$t)2+(6-$\frac{6}{5}$t)2=(2t)2,
化简得:13t2-90t+125=0,
解得:t1=5,t2=$\frac{25}{13}$,
∵当t=5时,AQ=10cm>AC,不合题意,舍去,
∴t=$\frac{25}{13}$,
∵当t=$\frac{25}{13}$时,S△AQP=$6t-\frac{6}{5}{t^2}$=6×$\frac{25}{13}$-$\frac{6}{5}$×($\frac{25}{13}$)2=$\frac{1200}{169}$cm2,
∴S菱形AQPQ′=2S△AQP=2×$\frac{1200}{169}$=$\frac{2400}{169}$cm2.
故存在时刻t=$\frac{25}{13}$s,使四边形AQPQ′为菱形,此时菱形的面积为$\frac{2400}{169}$cm2.
点评 本题属于四边形综合题,主要考查了菱形的性质,三角形的面积计算,勾股定理的逆定理,解一元二次方程以及相似三角形的性质和判定的综合应用,解决问题的关键是作辅助线构造相似三角形以及直角三角形,根据相似三角形的对应边成比例以及勾股定理进行列式求解.

 如图,点P位于点O的( )
如图,点P位于点O的( )| A. | 南偏西32° | B. | 北偏东32° | C. | 南偏东58° | D. | 北偏西58° |
| A. | 等于7 | B. | 小于7 | C. | 不小于7 | D. | 不大于7 |
 某课题组为了解全市九年级学生对数学知识的掌握情况,在一次数学检测中,从全市20000 名九年级考生中随机抽取部分学生的数学成绩进行调查,并将调查结果绘制成如图表:
某课题组为了解全市九年级学生对数学知识的掌握情况,在一次数学检测中,从全市20000 名九年级考生中随机抽取部分学生的数学成绩进行调查,并将调查结果绘制成如图表:| 分数段 | 频数 | 频率 |
| 50≤x≤60 | 20 | 0.10 |
| 60≤x≤70 | 28 | b |
| 70≤x≤80 | 54 | 0.27 |
| 80≤x≤90 | a | 0.20 |
| 90≤x≤100 | 24 | 0.12 |
| 100≤x≤110 | 18 | 0.09 |
| 110≤x≤120 | 16 | 0.08 |
(2)请在图中补全额数分布直方图;
(3)如果把成绩在70分以上(含70分)定为合格,那么该市20000名九年级考生数学成绩为合格的学生约有多少名?
| A. | 7、14 | B. | 8、16 | C. | 9、18 | D. | 10、20 |
 如图,点C是AB的中点,点D是BC的中点,则下列等式中正确的有( )
如图,点C是AB的中点,点D是BC的中点,则下列等式中正确的有( )