题目内容
 如图,在△ABC中,∠B=45°,BC=5,高AD=4,矩形EFPQ的一边QP在BC边上,E、F分别在AB、AC上,AD交EF于点H,设EF=x,
如图,在△ABC中,∠B=45°,BC=5,高AD=4,矩形EFPQ的一边QP在BC边上,E、F分别在AB、AC上,AD交EF于点H,设EF=x,(1)当x为何值时,矩形EFPQ是正方形;
(2)当x为何值时,矩形EFPQ的面积最大?并求出最大面积;
(3)当矩形EFPQ的面积最大时,该矩形EFPQ以每秒1个单位的速度沿射线DA匀速向上运动(当矩形的边PQ到达A点时停止运动),设运动时间为t秒,矩形EFPQ与△ABC重叠部分的面积为S,求S与t的函数关系式,并写出t的取值范围.
考点:相似三角形的判定与性质,二次函数的最值
专题:
分析:(1)由条件可得
=
,且AH=AD-HD,当矩形EFPQ为正方形时,有HD=EF=x,代入可求得x的值;
(2)可利用
=
,用x表示出HD,表示出矩形EFPQ的面积,利用二次函数可求得其最大值;
(3)当0≤t<2时,设矩形EFPQ与AB、AC的交点分别为M、N、R、S,可利用平行表示出MN的长,可表示出△EMS和△NFR的面积,进一步可表示出重叠部分的面积;当2≤t≤4时,重叠部分为△P′Q′A,利用平行分别用x表示出其底和高,可表示出面积.
| AH |
| AD |
| EF |
| BC |
(2)可利用
| AH |
| AD |
| EF |
| BC |
(3)当0≤t<2时,设矩形EFPQ与AB、AC的交点分别为M、N、R、S,可利用平行表示出MN的长,可表示出△EMS和△NFR的面积,进一步可表示出重叠部分的面积;当2≤t≤4时,重叠部分为△P′Q′A,利用平行分别用x表示出其底和高,可表示出面积.
解答:解:(1)∵四边形EFPQ为矩形,
∴EF∥BC,
∴
=
,
当矩形EFPQ为正方形时,HD=EF=x,
∴AH=AD-HD=4-x,且BC=5,
∴
=
,
解得x=
.
即当x为
时,矩形EFPQ为正方形;
(2)由(1)可知
=
,
∴HD=4-
x,
∴S矩形EFPQ=EF•FQ=EF•HD=x(4-
x)=-
x2+4x,
该函数为开口向下的二次函数,故当x=
时有最大值,最大值为5,
即当x为
时,矩形的面积有最大值5;
(3)由(2)可知,当矩形面积取最大值时,EF=
,FQ=2,
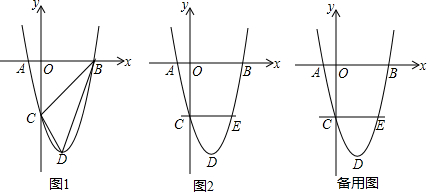
①当0≤t≤2时,如图1,设矩形与AB、AC分别交与点M、N、R、S,与AD交于J、L,连接RS,交AD于K,

由题意可知LD=JK=t,则AJ=AD-LD-JL=4-t-2=2-t,
又∵RS=
,
∴R、S为AB、AC的中点,
∴AK=
AD=2,ES=FR=JK=t,
又∵MN∥RS,
∴
=
,即
=
,
∴MN=
-
t,
∴EM+FN=EF-MN=
-(
-
t)=
t,
∴S△EMS+S△FNR=
ES(EM+FN)=
t•
t=
t2,
∴S=S矩形EFPQ-(S△EMS+S△FNR)=5-
t2;
②当2<t≤4时,如图2,设矩形与AB、AC、AD分别交于点Q′、P′、D′,

根据题意D′D=t,则AD′=4-t,
∵PQ∥BC,
∴
=
,即
=
,
解得P′Q′=5-
t,
∴S=S△AP′Q′=
P′Q′•AD′=
(4-t)(5-
t)=
t2-5t+10;
综上可知S=
.
∴EF∥BC,
∴
| AH |
| AD |
| EF |
| BC |
当矩形EFPQ为正方形时,HD=EF=x,
∴AH=AD-HD=4-x,且BC=5,
∴
| 4-x |
| 4 |
| x |
| 5 |
解得x=
| 20 |
| 9 |
即当x为
| 20 |
| 9 |
(2)由(1)可知
| 4-HD |
| 4 |
| x |
| 5 |
∴HD=4-
| 4 |
| 5 |
∴S矩形EFPQ=EF•FQ=EF•HD=x(4-
| 4 |
| 5 |
| 4 |
| 5 |
该函数为开口向下的二次函数,故当x=
| 5 |
| 2 |
即当x为
| 5 |
| 2 |
(3)由(2)可知,当矩形面积取最大值时,EF=
| 5 |
| 2 |
①当0≤t≤2时,如图1,设矩形与AB、AC分别交与点M、N、R、S,与AD交于J、L,连接RS,交AD于K,

由题意可知LD=JK=t,则AJ=AD-LD-JL=4-t-2=2-t,
又∵RS=
| 5 |
| 2 |
∴R、S为AB、AC的中点,
∴AK=
| 1 |
| 2 |
又∵MN∥RS,
∴
| AJ |
| AK |
| MN |
| RS |
| 2-t |
| 2 |
| MN | ||
|
∴MN=
| 5 |
| 2 |
| 5 |
| 4 |
∴EM+FN=EF-MN=
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 4 |
| 5 |
| 4 |
∴S△EMS+S△FNR=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 4 |
| 5 |
| 8 |
∴S=S矩形EFPQ-(S△EMS+S△FNR)=5-
| 5 |
| 8 |
②当2<t≤4时,如图2,设矩形与AB、AC、AD分别交于点Q′、P′、D′,

根据题意D′D=t,则AD′=4-t,
∵PQ∥BC,
∴
| P′Q′ |
| BC |
| AD′ |
| AD |
| P′Q′ |
| 5 |
| 4-t |
| 4 |
解得P′Q′=5-
| 5 |
| 4 |
∴S=S△AP′Q′=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 4 |
| 5 |
| 8 |
综上可知S=
|
点评:本题主要考查相似三角形的判定和性质及函数的性质,在(1)和(2)中分别用x表示出矩形的面积是解题的关键,在(3)中确定出重叠部分的图形是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若x≠y,则下列不能成立的等式是( )
| A、(x-y)2 =(y-x)2 |
| B、(x-y)3 =-(y-x)3 |
| C、(x+y)2 =(-x-y)2 |
| D、(x+y)2 =(-x+y)2 |
已知⊙O的半径是5,点A到圆心O的距离是7,则点A与⊙O的位置关系是( )
| A、点A在⊙O上 |
| B、点A在⊙O内 |
| C、点A在⊙O外 |
| D、点A与圆心O重合 |
 为了解某校1800名学生对新闻、体育、动画、娱乐四类电视节目的喜爱情况,随机抽取部分学生进行调查,结果如图,则该校喜爱体育节目的学生大约有
为了解某校1800名学生对新闻、体育、动画、娱乐四类电视节目的喜爱情况,随机抽取部分学生进行调查,结果如图,则该校喜爱体育节目的学生大约有