题目内容
14. 如图,直径为10的⊙A经过点C(0,5)和点O (0,0),B是y轴右侧⊙A优弧上一点,则tan∠OBC的值为( )
如图,直径为10的⊙A经过点C(0,5)和点O (0,0),B是y轴右侧⊙A优弧上一点,则tan∠OBC的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\sqrt{3}$ |
分析 首先设⊙A与x轴的另一个交点为D,连接CD,根据直角对的圆周角是直径,即可得CD是直径,又由在同圆或等圆中,同弧或等弧所对的圆周角相等,可得∠OBC=∠ODC,继而可求得答案.
解答  解:设⊙A与x轴的另一个交点为D,连接CD,
解:设⊙A与x轴的另一个交点为D,连接CD,
∵∠COD=90°,
∴CD是直径,即CD=10,
∵C(0,5),
∴OC=5,
∴OD=$\sqrt{{CD}^{2}-{OC}^{2}}$=5$\sqrt{3}$,
∵∠OBC=∠ODC,
∴tan∠OBC=tan∠ODC=$\frac{OC}{OD}$=$\frac{5}{5\sqrt{3}}$=$\frac{\sqrt{3}}{3}$.
故选C.
点评 此题考查了圆周角定理、勾股定理以及三角函数的定义.注意掌握辅助线的作法,注意掌握数形结合思想与转化思想的应用.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
4.下表是某种抽奖活动中,封闭的抽奖箱中各种球的颜色、数量,以及它们所代表的奖项:
为了保证抽奖的公平性,这些小球除了颜色外,其他都相同,而且每一个球被抽中的机会均相等,则该抽奖活动抽中一等奖的概率为( )
| 颜色 | 数量(个) | 奖项 |
| 红色 | 5 | 一等奖 |
| 黄色 | 6 | 二等奖 |
| 蓝色 | 9 | 三等奖 |
| 白色 | 10 | 四等奖 |
| A. | $\frac{1}{6}$ | B. | $\frac{1}{5}$ | C. | $\frac{3}{10}$ | D. | $\frac{1}{2}$ |
5.分式$\frac{|x|-4}{x+4}$的值为0,则x的值为( )
| A. | 4 | B. | -4 | C. | ±4 | D. | 任意实数 |
9.若分式$\frac{{{x^2}-1}}{x+1}$的值为零,则x的值为( )
| A. | 0 | B. | 1 | C. | -1 | D. | ±1 |
3.化简$\frac{{{a^2}-1}}{{{a^2}+2a+1}}÷\frac{a-1}{a}$的结果是( )
| A. | $\frac{1}{2}$ | B. | $\frac{a}{a+1}$ | C. | $\frac{a+1}{a}$ | D. | $\frac{a+1}{a+2}$ |
9.关于x的一元二次方程ax2-x+1=0有实数根,则a的取值范围是( )
| A. | a≤$\frac{1}{4}$且a≠0 | B. | a≤$\frac{1}{4}$ | C. | a≥$\frac{1}{4}$且a≠0 | D. | a≥$\frac{1}{4}$ |
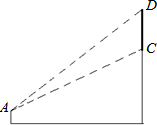 合肥新桥国际机场出港大厅有一幅“黄山胜景”的壁画.聪聪站在距壁画水平距离15米的地面,自A点看壁画上部D的仰角为45°,看壁画下部C的仰角为30°,求壁画CD的高度.(参考数据:$\sqrt{3}$≈1.7,$\sqrt{2}$≈1.4,精确到十分位)
合肥新桥国际机场出港大厅有一幅“黄山胜景”的壁画.聪聪站在距壁画水平距离15米的地面,自A点看壁画上部D的仰角为45°,看壁画下部C的仰角为30°,求壁画CD的高度.(参考数据:$\sqrt{3}$≈1.7,$\sqrt{2}$≈1.4,精确到十分位)