题目内容
15．
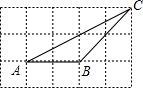如图，每个小正方形的边长为1，△ABC的顶点都在方格纸的格点上，则sinA=$\frac{\sqrt{5}}{5}$．
分析 根据勾股定理，可得AC的长，根据锐角三角函数的正弦于等对边比斜边，可得答案．
解答 解：如图：
，
由勾股定理，得
AC=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$，
sinA=$\frac{CD}{AC}$=$\frac{2}{2\sqrt{5}}$=$\frac{\sqrt{5}}{5}$，
故答案为：$\frac{\sqrt{5}}{5}$．
点评 本题考查了锐角三角函数的定义，锐角三角函数的正弦等于对边比斜边，余弦等于邻边比斜边，正切等于对边比邻边．
练习册系列答案
阅读快车系列答案
相关题目
5．分式$\frac{|x|-4}{x+4}$的值为0，则x的值为（ ）
| A． | 4 | B． | -4 | C． | ±4 | D． | 任意实数 |
3．化简$\frac{{{a^2}-1}}{{{a^2}+2a+1}}÷\frac{a-1}{a}$的结果是（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{a}{a+1}$ | C． | $\frac{a+1}{a}$ | D． | $\frac{a+1}{a+2}$ |
20．下列命题是假命题的是（ ）
| A． | 平行四边形的对边相等 | |
| B． | 对角线互相平分的四边形是平行四边形 | |
| C． | 四条边都相等的四边形是菱形 | |
| D． | 矩形的对角线互相垂直 |
9．关于x的一元二次方程ax2-x+1=0有实数根，则a的取值范围是（ ）
| A． | a≤$\frac{1}{4}$且a≠0 | B． | a≤$\frac{1}{4}$ | C． | a≥$\frac{1}{4}$且a≠0 | D． | a≥$\frac{1}{4}$ |