题目内容
17.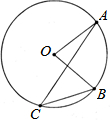 如图,⊙O上A、B、C三点,若∠B=50°,∠A=20°,则∠AOB等于( )
如图,⊙O上A、B、C三点,若∠B=50°,∠A=20°,则∠AOB等于( )| A. | 30° | B. | 50° | C. | 70° | D. | 60° |
分析 先根据圆周角定理得出∠ACB=$\frac{1}{2}$∠AOB,再由三角形内角和定理即可得出结论.
解答 解:∵∠AOB与∠ACB是同弧所对的圆心角与圆周角,∠B=50,∠A=20°,
∴∠ACB=$\frac{1}{2}$∠AOB.
∴180°-∠AOB-∠A=180°-∠ACB-∠B,即180°-∠AOB-20°=180°-$\frac{1}{2}$∠AOB-50°,
解得∠AOB=60°.
故选D.
点评 本题考查的是圆周角定理,熟知在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半是解答此题的关键.

练习册系列答案
相关题目
8.某中学随机调查了15名学生,了解他们一周在校的体育锻炼时间,结果如下表所示:
那么这15名学生这一周在校参加体育锻炼的时间的众数是7小时.
| 一周在校的体育锻炼时间(小时) | 5 | 6 | 7 | 8 |
| 人数 | 2 | 5 | 6 | 2 |
5.分式$\frac{|x|-4}{x+4}$的值为0,则x的值为( )
| A. | 4 | B. | -4 | C. | ±4 | D. | 任意实数 |
12.下列计算正确的是( )
| A. | a2+a2=a4 | B. | (a2)3=a5 | C. | 2a-a=2 | D. | (ab)2=a2b2 |
9.若分式$\frac{{{x^2}-1}}{x+1}$的值为零,则x的值为( )
| A. | 0 | B. | 1 | C. | -1 | D. | ±1 |