题目内容
13.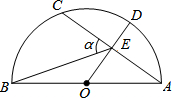 如图,AB是半圆的直径,点O为圆心,OA=5,弦AC=8,OD⊥AC,垂足为E,交⊙O于D,连续BE,设∠BEC=α,则cosa的值为$\frac{2\sqrt{13}}{13}$.
如图,AB是半圆的直径,点O为圆心,OA=5,弦AC=8,OD⊥AC,垂足为E,交⊙O于D,连续BE,设∠BEC=α,则cosa的值为$\frac{2\sqrt{13}}{13}$.
分析 首先连接BC,根据AB为⊙O直径,可得∠BCA=90°,在Rt△ABC中,由勾股定理,求出BC的长度是多少;然后在Rt△BCE中,由勾股定理,求出BE的长度是多少;最后根据一个角的正弦的求法,求出sinα的值为多少即可.
解答  解:如图,连接BC,
解:如图,连接BC,
∵AB为⊙O直径,
∴∠BCA=90°,
又∵AB=2OA=10,AC=8,
∴BC=6,
又∵OD⊥AC,
∴CE=AE=4,
在Rt△BCE中,由勾股定理得
BE=$\sqrt{B{C}^{2}+E{C}^{2}}$=$\sqrt{{6}^{2}+{4}^{2}}$=2$\sqrt{13}$,
∴cosa=$\frac{CE}{BE}$=$\frac{4}{2\sqrt{13}}$=$\frac{2\sqrt{13}}{13}$.
故答案为:$\frac{2\sqrt{13}}{13}$.
点评 此题主要考查了圆周角定理的应用,解答此题的关键是要明确:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.还考查了直角三角形的性质的应用,以及勾股定理的应用,还考查了锐角三角函数的定义以及求法,要熟练掌握.

练习册系列答案
相关题目
8.抛物线y=(x-1)(x+3)顶点坐标是( )
| A. | (2,5) | B. | (-22,-3) | C. | (1,0) | D. | (-1,-4) |
2.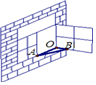 如图,一扇窗户打开后,用窗钩AB可将其固定,这里所运用的几何原理是( )
如图,一扇窗户打开后,用窗钩AB可将其固定,这里所运用的几何原理是( )
 如图,一扇窗户打开后,用窗钩AB可将其固定,这里所运用的几何原理是( )
如图,一扇窗户打开后,用窗钩AB可将其固定,这里所运用的几何原理是( )| A. | 垂线段最短 | B. | 两点之间线段最短 | ||
| C. | 两点确定一条直线 | D. | 三角形的稳定性 |
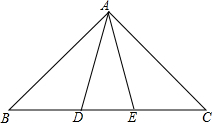 如图,△ABC中,AB=AC,点D,E在边BC上,且BD=CE.
如图,△ABC中,AB=AC,点D,E在边BC上,且BD=CE.