题目内容
1.如果有理数a、b满足(a-3)2+|b+1|=0,那么ba=-1.分析 根据非负数的性质列式求出a、b的值,然后代入代数式进行计算即可得解.
解答 解:由题意得,a-3=0,b+1=0,
解得a=3,b=-1,
所以,ba=(-1)3=-1.
故答案为:-1.
点评 本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
12.一元二次方程x2+2x+4=0的根的情况是( )
| A. | 有两个相等的实数根 | B. | 有两个不相等的实数根 | ||
| C. | 只有一个实数根 | D. | 没有实数根 |
6.已知∠A是锐角,且sinA=$\frac{1}{2}$,则tanA的值是( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
10.我市从2017年1月1日起连续七天空气质量堪忧,PM2.5大于300时为严重污染,下表是这几天的Pm2.5空气质量指数
则这组数据的中位数和平均数分别为( )
| 日期 | 1号 | 2号 | 3号 | 4号 | 5号 | 6号 | 7号 |
| 空气质量指数 | 446 | 402 | 456 | 499 | 500 | 434 | 105 |
| A. | 446,416 | B. | 446,406 | C. | 451,406 | D. | 499,416 |
11.某公司在销售一种产品进价为10元的产品时,每年总支出为10万元(不含进货支出),经过若干年销售得知,年销售量y(万件)是销售单价x(元)的一次函数,并得到如下部分数据;
(1)求出y关于x的函数关系式是y=-$\frac{1}{2}$x+13;
(2)写出该公司销售这种产品的年利润w(万元)关于销售单价x(元)的函数关系式;当销售单价x为何值时,年利润最大?
(3)试通过(2)中的函数关系式及其大致图象,帮助该公司确定产品的销售单价范围,使年利润不低于20万元(请直接写出销售单价x的范围).
| 销售单价x(元) | 12 | 14 | 16 | 18 |
| 年销售量y(万件) | 7 | 6 | 5 | 4 |
(2)写出该公司销售这种产品的年利润w(万元)关于销售单价x(元)的函数关系式;当销售单价x为何值时,年利润最大?
(3)试通过(2)中的函数关系式及其大致图象,帮助该公司确定产品的销售单价范围,使年利润不低于20万元(请直接写出销售单价x的范围).




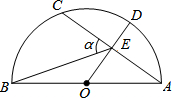 如图,AB是半圆的直径,点O为圆心,OA=5,弦AC=8,OD⊥AC,垂足为E,交⊙O于D,连续BE,设∠BEC=α,则cosa的值为$\frac{2\sqrt{13}}{13}$.
如图,AB是半圆的直径,点O为圆心,OA=5,弦AC=8,OD⊥AC,垂足为E,交⊙O于D,连续BE,设∠BEC=α,则cosa的值为$\frac{2\sqrt{13}}{13}$.