题目内容
如图1,在△ABC中,AB=AC,D为BC边上一点,DE⊥AB于E,DF⊥AC于F
作图:请作出AC边上的高BG
探究:
(1)请你通过观察、测量找到DE、DF、BG之间的数量关系:
(2)为了说明DE、DF、BG之间的数量关系,小嘉是这样做的:
连接AD
则S△ADC= ,S△ABD=
∴S△ABC=
S△ABC还可以表示为
…
请你帮小嘉完成上述填空
拓展:如图2,当D在如图2的位置时,上面DE、DF、BG之间的数量关系是否仍然成立?并说明理由
作图:请作出AC边上的高BG
探究:
(1)请你通过观察、测量找到DE、DF、BG之间的数量关系:
(2)为了说明DE、DF、BG之间的数量关系,小嘉是这样做的:
连接AD
则S△ADC=
∴S△ABC=
S△ABC还可以表示为
…
请你帮小嘉完成上述填空
拓展:如图2,当D在如图2的位置时,上面DE、DF、BG之间的数量关系是否仍然成立?并说明理由

考点:等腰三角形的性质,三角形的面积
专题:探究型
分析:(1)作出AC边上的高BG,连接AD,分别求出△ABD、△ADC与△ABC的面积,进而可得出结论;
(2)根据(1)中的证明过程可得出结论.
(2)根据(1)中的证明过程可得出结论.
解答: 解:如图所示:
解:如图所示:
(1)BG=DE+DF,
连接AD,
∵DE⊥AB于E,DF⊥AC于F,AB=AC,
∴S△ABC=S△ABD+S△ACD=
AB•DE+
AC•DF=
AC•(DE+DF),
∵BG⊥AC,
∴S△ABC=
AC•BG,
∴BG=DE+DF.
故答案为:BG=DE+DF;
(2)由(1)可知,S△ADC=
AC•DF,S△ABD=
AB•DE
∴S△ABC=
AC•DF+
AB•DE
S△ABC还可以表示为
AC•BG.
故答案为:
AC•DF,
AB•DE,
AC•DF+
AB•DE,
AC•BG
拓展结论仍然成立,即BG=DE+DF.
 解:如图所示:
解:如图所示:(1)BG=DE+DF,
连接AD,
∵DE⊥AB于E,DF⊥AC于F,AB=AC,
∴S△ABC=S△ABD+S△ACD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵BG⊥AC,
∴S△ABC=
| 1 |
| 2 |
∴BG=DE+DF.
故答案为:BG=DE+DF;
(2)由(1)可知,S△ADC=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
S△ABC还可以表示为
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
拓展结论仍然成立,即BG=DE+DF.
点评:本题考查的是等腰三角形的性质、三角形的面积等知识,难度适中.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知y=
+
-3,则xy=( )
| x-5 |
| 10-2x |
| A、-15 | B、-9 | C、9 | D、15 |
如果a<b,那么下列不等式成立的是( )
| A、a-b>0 | ||||
| B、a-3>b-3 | ||||
C、
| ||||
| D、-3a>-3b |
下列运算正确的是( )
| A、3a-2a=1 |
| B、(x-1)(1-x)=1-x2 |
| C、(a-2)2=a2-4 |
| D、2a-3a=-a |
下列计算正确的是( )
| A、x2•x3=x6 |
| B、(x3)2=x9 |
| C、x12÷x3=x4 |
| D、(x2+1)0=1 |
 如图,在平面直角坐标系xOy中,一次函数y1=-x-1的图象与x轴交于点A,与y轴交于点B,与反比例函数y2=
如图,在平面直角坐标系xOy中,一次函数y1=-x-1的图象与x轴交于点A,与y轴交于点B,与反比例函数y2=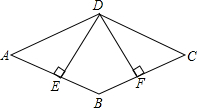 如图,四边形ABCD是菱形,DE⊥AB于E,EF⊥BC于F.求证:DE=DF.
如图,四边形ABCD是菱形,DE⊥AB于E,EF⊥BC于F.求证:DE=DF.