题目内容
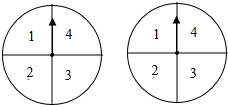
现有一项资助贫困生的公益活动,每位参与者需交赞助费5元,活动规则如下:如图是两个可以自由转动的转盘,每个转盘被分成4个相等的扇形,参与者转动这两个转盘,转盘停止后,指针各自指向一个数字,(若指针在分格线上,则重转一次,直到指针指向某一数字为止),若指针最后所指的数字之和为8,则获得一等奖,奖金16元;若指针最后所指的数字之和为7,则获得二等奖,奖金8元;若指针最后所指的数字之和为6,则获得三等奖,奖金为4元;其余均不得奖;此次活动所集到的赞助费除支付获奖人员的奖金外,其余全部用于资助贫困生的学习和生活;
(1)分别求出此次活动中获得一等奖、二等奖、三等奖的概率;
(2)若此次活动有2000人参加,请你估计此次活动结束后有多少赞助费用于资助贫困生?
(1)分别求出此次活动中获得一等奖、二等奖、三等奖的概率;
(2)若此次活动有2000人参加,请你估计此次活动结束后有多少赞助费用于资助贫困生?

考点:列表法与树状图法
专题:
分析:(1)此题需要两步完成,所以采用树状图法或者采用列表法都比较简单;解题时要注意是放回实验还是不放回实验,此题属于不放回实验.列举出符合题意的各种情况的个数,再根据概率公式解答即可.
(2)总费用减去奖金即为所求的金额.
(2)总费用减去奖金即为所求的金额.
解答:解:(1)所有出现的情况如下,
∴一共有16种情况,此次活动中获得一等奖、二等奖、三等奖的分别有1,2,3种情况,
∴P(一等奖)=
,P( 二等奖)=
,P(三等奖)=
,
(2)2000×
×16+2000×
×8+2000×
×4=5500(元),5×2000-5500=4500(元)
答:此次活动结束后有4500元赞助费用于资助贫困生.
| 和 | 1 | 2 | 3 | 4 |
| 1 | 2 | 3 | 4 | 5 |
| 2 | 3 | 4 | 5 | 6 |
| 3 | 4 | 5 | 6 | 7 |
| 4 | 5 | 6 | 7 | 8 |
∴P(一等奖)=
| 1 |
| 16 |
| 1 |
| 8 |
| 3 |
| 16 |
(2)2000×
| 1 |
| 16 |
| 1 |
| 8 |
| 3 |
| 16 |
答:此次活动结束后有4500元赞助费用于资助贫困生.
点评:本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件,用到的计算公式为:p=
.
| m |
| n |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列计算正确的是( )
| A、x2•x3=x6 |
| B、(x3)2=x9 |
| C、x12÷x3=x4 |
| D、(x2+1)0=1 |
 某学校为了加强学生的安全意识,组织了1500名学生参加安全知识竞赛,从中抽取了部分学生成绩(得分取正整数,满分为100分)进行统计,请根据如图的频数分布表和尚未完成的频数分布直方图,解答下列问题:
某学校为了加强学生的安全意识,组织了1500名学生参加安全知识竞赛,从中抽取了部分学生成绩(得分取正整数,满分为100分)进行统计,请根据如图的频数分布表和尚未完成的频数分布直方图,解答下列问题: 如图,直线y=-x+1与x,y轴分别交于A、B两点,P(a,b)为双曲线y=
如图,直线y=-x+1与x,y轴分别交于A、B两点,P(a,b)为双曲线y=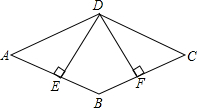 如图,四边形ABCD是菱形,DE⊥AB于E,EF⊥BC于F.求证:DE=DF.
如图,四边形ABCD是菱形,DE⊥AB于E,EF⊥BC于F.求证:DE=DF.