题目内容
已知y=y1+y2,y1与x成正比例,y2与x-2成正比例,且当x=1时,y=-1;x=4时,y=20,求当x=-3时,y的值.
考点:待定系数法求一次函数解析式
专题:
分析:设y1=ax,y2=k(x-2),由当x=1时,y=-1.当x=4时,y=20可得关于a、k的两个等式联立方程组即可求出a,k,得出y的表达式,然后把x=-3代入求解即可.
解答:解:设y1=ax,y2=k(x-2),则y=ax+k(x-2),
∵当x=1时,y=-1.当x=4时,y=20,
∴
,解得
,
∴y=3x+4(x-2)=7x-8
把x=-3代入函数可得:y=-3×7-8=-29.
∵当x=1时,y=-1.当x=4时,y=20,
∴
|
|
∴y=3x+4(x-2)=7x-8
把x=-3代入函数可得:y=-3×7-8=-29.
点评:本题考查了待定系数法求解析式以及求函数值,熟练掌握正比例函数的性质是关键.

练习册系列答案
相关题目
下列说法不正确的是( )
| A、a2•a4=a6 |
| B、a3•a3=a6 |
| C、(-x)2•(-x)3=(-x)5 |
| D、z2•z3=z6 |
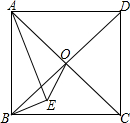 如图,在正方形ABCD内有一点E,∠AEB=90°,AE=2
如图,在正方形ABCD内有一点E,∠AEB=90°,AE=2