题目内容
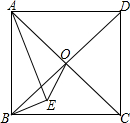 如图,在正方形ABCD内有一点E,∠AEB=90°,AE=2
如图,在正方形ABCD内有一点E,∠AEB=90°,AE=2| 5 |
考点:正方形的性质,全等三角形的判定与性质
专题:
分析:延长BE到F,使BF=AE,连接OF,作OG⊥BE,交BE的延长线于G,根据SAS求得△OAE≌△OBF,得出OE=OF,∠AOE=∠BOF,进而求得△EOF是等腰直角三角形,根据勾股定理和直角三角形的性质求得EF=2
,OG=
,根据三角形的面积公式即可求得三角形BEO的面积;
| 2 |
| 2 |
解答: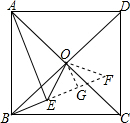 解:延长BE到F,使BF=AE,连接OF,作OG⊥BE,交BE的延长线于G,
解:延长BE到F,使BF=AE,连接OF,作OG⊥BE,交BE的延长线于G,
∵四边形ABCD是正方形,
∴OA=OB,∠AOB=90°,
∵∠AEB=∠BOC=90°,
∴∠OBE=∠EAO,
在△OAE和△OBF中,
,
∴△OAE≌△OBF(SAS),
∴OE=OF,∠AOE=∠BOF,
∴∠AOE-∠AOB=∠BOF-∠BOC,即∠BOE=∠COF,
∴∠BOC=∠BOE+∠EOC=∠COF+∠EOC=90°,
∴△EOF是等腰直角三角形,
∵OE=OF=2,
∴EF=2
,OG=
,
∴BE=BF-EF=2
-2
,
∴S△BEO=
BE•OG=
×(2
-2
)×
=
-2
故答案为:
-2.
 解:延长BE到F,使BF=AE,连接OF,作OG⊥BE,交BE的延长线于G,
解:延长BE到F,使BF=AE,连接OF,作OG⊥BE,交BE的延长线于G,∵四边形ABCD是正方形,
∴OA=OB,∠AOB=90°,
∵∠AEB=∠BOC=90°,
∴∠OBE=∠EAO,
在△OAE和△OBF中,
|
∴△OAE≌△OBF(SAS),
∴OE=OF,∠AOE=∠BOF,
∴∠AOE-∠AOB=∠BOF-∠BOC,即∠BOE=∠COF,
∴∠BOC=∠BOE+∠EOC=∠COF+∠EOC=90°,
∴△EOF是等腰直角三角形,
∵OE=OF=2,
∴EF=2
| 2 |
| 2 |
∴BE=BF-EF=2
| 5 |
| 2 |
∴S△BEO=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 2 |
| 10 |
故答案为:
| 10 |
点评:本题考查了正方形的性质,等腰直角三角形的判定和性质,勾股定理的应用,三角形全等的判定和性质以及三角形面积的计算,作出辅助线构建全等三角形是本题的关键.

练习册系列答案
相关题目