题目内容
15. 完成下面的证明(下划线内补全证明过程,括号内填写推理的依据).
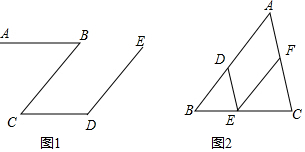
完成下面的证明(下划线内补全证明过程,括号内填写推理的依据).(1)如图1,AB∥CD,∠B+∠D=180°,求证:CB∥DE
证明:∵AB∥CD(已知)
∴∠B=∠C
∵∠B+∠D=180°(已知)
∴∠C+∠D=180°(等量代换)
∴CB∥DE
(2)如图2,已知DE∥AC,∠A=∠DEF,请证明∠B=∠FEC.
证明:∵DE∥AC(已知)
∴∠A=∠BDE
∵∠A=∠DEF(已知)
∴∠DEF=∠BDE(等量代换)
∴AB∥EF
∴∠B=∠FEC.
分析 (1)先根据平行线的性质得出∠B=∠C,再由∠B+∠D=180°可得出∠C+∠D=180°,据此可得出结论;
(2)先根据DE∥AC得出∠A=∠BDE,再由∠A=∠DEF可得出∠DEF=∠BDE,据此可得出结论.
解答 (1)证明:∵AB∥CD(已知),
∴∠B=∠C.
∵∠B+∠D=180°(已知)
∴∠C+∠D=180°(等量代换)
∴CB∥DE.
故答案为:∠C;CB,DE;
(2)证明:∵DE∥AC(已知),
∴∠A=∠BDE.
∵∠A=∠DEF(已知)
∴∠DEF=∠BDE(等量代换)
∴AB∥EF,
∴∠B=∠FEC.
故答案为:∠BDE;BDE;EF;B,FEC.
点评 本题考查的是平行线的判定与性质,熟知平行线的判定定理是解答此题的关键.

练习册系列答案
相关题目
6.下列调查中,适宜采用全面调查(普查)方式的是( )
| A. | 了解我国民众对“乐天萨德事件”的看法 | |
| B. | 了解浙江卫视“奔跑吧兄弟”节目的收视率 | |
| C. | 调查我校某班学生喜欢上数学课的情况 | |
| D. | 调查某类烟花爆竹燃放的安全情况 |
10.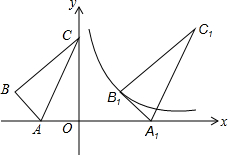 如图,△ABC的顶点A,C落在坐标轴上,且顶点B的坐标为(-5,2),将△ABC沿x轴向右平移得到△A1B1C1,使得点B1恰好落在函数y=$\frac{6}{x}$上,若线段AC扫过的面积为48,则点C1的坐标为( )
如图,△ABC的顶点A,C落在坐标轴上,且顶点B的坐标为(-5,2),将△ABC沿x轴向右平移得到△A1B1C1,使得点B1恰好落在函数y=$\frac{6}{x}$上,若线段AC扫过的面积为48,则点C1的坐标为( )
 如图,△ABC的顶点A,C落在坐标轴上,且顶点B的坐标为(-5,2),将△ABC沿x轴向右平移得到△A1B1C1,使得点B1恰好落在函数y=$\frac{6}{x}$上,若线段AC扫过的面积为48,则点C1的坐标为( )
如图,△ABC的顶点A,C落在坐标轴上,且顶点B的坐标为(-5,2),将△ABC沿x轴向右平移得到△A1B1C1,使得点B1恰好落在函数y=$\frac{6}{x}$上,若线段AC扫过的面积为48,则点C1的坐标为( )| A. | (3,2) | B. | (5,6) | C. | (8,6) | D. | (6,6) |
7.如果x-2y=5,xy=-2,那么(x+2y)2=( )
| A. | 17 | B. | 21 | C. | 23 | D. | 9 |
14.据报道,2016年深圳双创活动周上会场参观人数累计超过50万人,某数学学习兴趣小组为了解参观者的职业情况,他们应采用的收集数据的方式是( )
| A. | 对所有参观者发放问卷进行调查 | |
| B. | 对所有参观者中的成年人发放问卷进行调查 | |
| C. | 在主会场入口随机发放问卷进行调查 | |
| D. | 在无人机展厅随机发放问卷进行调查 |
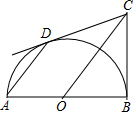 如图所示,AB是半圆O的直径,∠ABC=90°,点D是半圆O上一动点(不与点A、B重合),且AD∥CO.
如图所示,AB是半圆O的直径,∠ABC=90°,点D是半圆O上一动点(不与点A、B重合),且AD∥CO.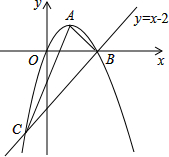 如图,已知抛物线经过原点O,顶点为A(1,1),且与直线y=x-2交于B,C两点.
如图,已知抛物线经过原点O,顶点为A(1,1),且与直线y=x-2交于B,C两点.